《铁路工程结构可靠性设计统一标准[附条文说明]》GB 50216-2019

中华人民共和国国家标准

铁路工程结构可靠性设计统一标准

Unified standard for reliability design of railway structures

GB 50216-2019

主编部门：国家铁路局

批准部门：中华人民共和国住房和城乡建设部

施行日期：2020年6月1日

中华人民共和国住房和城乡建设部公告

2019年 第322号

住房和城乡建设部关于发布国家标准《铁路工程结构可靠性设计统一标准》的公告

现批准《铁路工程结构可靠性设计统一标准》为国家标准，编号为GB 50216-2019，自2020年6月1日起实施。其中，第3.2.1、3.3.1条为强制性条文，必须严格执行。原《铁路工程结构可靠度设计统一标准》(GB 50216-94)同时废止。

本标准在住房和城乡建设部门户网站(www.mohurd.gov.cn)公开，并由住房和城乡建设部标准定额研究所组织中国计划出版社出版发行。

中华人民共和国住房和城乡建设部

2019年11月22日

前言

根据住房和城乡建设部《关于印发<2015年工程建设标准规范制订、修订计划>的通知》(建标[2014]189号)要求，标准编制组经过广泛调查研究，认真总结经验，参考有关国际标准和国外先进标准，并在广泛征求意见的基础上，对国家标准《铁路工程结构可靠度设计统一标准》GB 50216-94进行了全面修订。

本标准的主要技术内容是：总则、术语和符号、基本规定、极限状态设计原则、作用及环境影响、材料和岩土的性能及几何参数、结构分析和试验辅助设计、分项系数设计方法、可靠性管理及评定等。

本标准修订的主要技术内容是：1.适用范围调整为铁路桥涵、隧道、路基、轨道等工程结构和构件的设计及其既有结构的可靠性评定。2.增加了评估使用年限、疲劳极限状态、分位值、特征值、岩土作用、环境影响等术语，删除了脆性破坏、延性破坏、疲劳承载能力极限状态、疲劳正常使用极限状态等常识性或不再使用的术语。3.完善了铁路工程结构的安全等级划分和设计使用年限，给出了工程结构可靠性水平的设置、耐久性和维护的原则性规定。4.细化和完善了极限状态的分类，明确了铁路工程结构按承载能力极限状态、正常使用极限状态和疲劳极限状态进行设计。增加了地震设计状况的分类，给出了基于可靠指标设计的原则性规定。5.增加了列车竖向作用的相关规定。6.完善了材料性能的取值要求，明确了岩土性能标准值的确定方法。7.增加了试验辅助设计的相关规定。8.增加了铁路桥涵结构列车荷载作用分项系数的取值规定，完善了结构抗力和作用效应设计值的计算式，补充规定了结构重要性系数的取值。9.明确了全寿命周期的质量管理，增加了既有结构可靠性评定的原则性要求。

本标准中以黑体字标志的条文为强制性条文，必须严格执行。

本标准由住房和城乡建设部负责管理和对强制性条文的解释，由中国铁道科学研究院集团有限公司负责具体技术内容的解释。执行过程中如有意见或建议，请寄送中国铁道科学研究院集团有限公司(地址：北京市海淀区大柳树路2号，邮政编码：100081)。

本标准主编单位：中国铁道科学研究院集团有限公司

本标准参编单位：中国铁路经济规划研究院有限公司

中铁第一勘察设计院集团有限公司

中国中铁二院工程集团有限责任公司

中国铁路设计集团有限公司

中铁第四勘察设计院集团有限公司

中铁工程设计咨询集团有限公司

本标准主要起草人员：刘晓光 潘永杰 张玉玲 徐升桥 周诗广 杨常所 余鹏 许国平 王仲锦 林传年 刘华 杜宝军 费建波 苏伟 葛建军 高策 高志伟 赵东平 罗一农 孙立 蒋函珂 周勇政 简方梁 陈潇 霍建勋 乔晋飞

本标准主要审查人员：李承根 史志华 薛吉岗 刘燕 杨鹏健 江成 赵万强 王召祜 李安洪 吴少海 张红旭 周四思 曾长贤 郜永杰 杜文山 柳墩利 李纹京 季文玉 杨剑 宋玉香 杨彦海 范佳 刘建瑞 吴川 朱尔玉 徐伟 韩晓强 王伟华 卢朝辉

1.0.1  为统一铁路工程结构可靠性设计的基本原则、基本要求和基本方法，使铁路工程符合可持续发展的要求，并做到安全可靠、技术先进、经济合理、确保质量，制定本标准。

▼ 展开条文说明
1.0.1  本标准对铁路工程结构可靠性设计的基本原则、基本要求和基本方法做出了统一规定，目的是实现结构设计的安全可靠、技术先进、经济合理、确保质量和可持续发展的要求，使铁路工程结构设计能够满足确保人的生命和财产安全并符合国家技术经济政策的要求。
与可持续发展相关的性能指标包括但不限于环境质量、成本效率、二氧化碳排放最小化、自然资源／能源消耗最小化、绿色低碳等。

1.0.2  本标准适用于铁路桥涵、隧道、路基、轨道等工程结构和构件的设计及其既有结构的可靠性评定。

▼ 展开条文说明
1.0.2  本条规定了本标准的适用范围。本标准作为我国铁路工程结构领域的一本基础标准，所规定的基本原则、基本要求和基本方法适用于桥涵、隧道、路基、轨道等结构及其构件的设计，包括过程阶段的设计变更，也适用于既有结构的可靠性评定。

1.0.3  铁路工程结构设计宜采用以概率理论为基础、以分项系数表达的极限状态设计方法；当缺乏统计资料时，可根据可靠的工程经验或必要的试验研究，采用其他设计方法进行设计。

▼ 展开条文说明
1.0.3  以概率理论为基础、以分项系数表达的极限状态设计方法已广泛应用到国内外工程结构设计领域中，适用于失效和损坏后果已非常明确及失效模式可用标准化方式分类和模拟的结构，是我国铁路工程结构设计方法的发展趋势。
概率极限状态设计法是以大量的统计资料为基础，原则上使所有已知的不确定性得到量化。考虑到不同工程结构所具有的统计数据在质与量两个方面存在较大差异，有些甚至没有统计数据，因而规定当缺乏统计资料，无法采用可靠指标来表征结构可靠度时，工程结构设计可按其他设计方法(如容许应力法)进行，也可根据工程经验或通过必要的试验确定。

1.0.4  制定铁路工程结构的可靠性设计相关标准时，应符合本标准的规定。

▼ 展开条文说明
1.0.4  本标准规定了铁路工程结构可靠性设计相关标准需遵守的基本准则，并不能代替各类结构设计标准和其他相关标准(三层次规范)。如从结构设计看，本标准主要制定了铁路工程结构设计各种基本变量的取值原则、作用组合的规则、作用组合效应的确定方法等。基本变量的具体取值及在各种受力状态下作用效应和结构抗力的具体计算方法，仍由各类工程结构的设计标准和其他相关标准做出相应规定。

1.0.5  铁路工程结构的勘察设计、施工、使用与维护应进行有效的质量管理与控制，使结构满足规定的可靠性要求。

▼ 展开条文说明
1.0.5  结构可靠性的保证是以正常设计、正常施工和正常维护为基础。结构的失效概率在寿命周期内服从浴盆曲线分布，结构可靠性上限是由设计确定的，在施工前期和使用后期失效风险变大，当进行维修养护时，可靠性会增长，结构可靠性与全寿命周期工程行为息息相关。因此，为了确保工程结构的安全性、适用性和耐久性，应对结构寿命全过程的各个阶段进行质量管理和控制。

1.0.6  铁路工程结构可靠性设计除应符合本标准要求外，尚应符合国家现行有关标准的规定。

▼ 展开条文说明
1.0.6  本标准属于第二层次标准，铁路工程结构设计还应符合国家现行的其他标准规定。

2.1.1  可靠性    reliability

   结构在规定的时间内，在规定的条件下，完成预定功能的能力。

2.1.2  可靠度  degree of reliability

   结构在规定的时间内，在规定的条件下，完成预定功能的概率。

2.1.3  失效概率  probability of failure

   结构在规定的时间内，在规定的条件下，不能完成预定功能的概率。

2.1.4  可靠指标    reliability index

   度量结构可靠度的数值指标，可靠指标β与失效概率Pf的关系为β＝—Φ-1(Pf)，其中Φ-1(·)为标准正态分布函数的反函数。

2.1.5  设计使用年限  design working life

   正常使用和维护条件下，设计规定的结构或构件不需进行大修即可按预定目的使用的年限。

2.1.6  设计基准期  design reference period

   为确定可变作用等的取值而选用的时间参数。

2.1.7  评估使用年限  assessed working life

   可靠性评定所预估的既有结构在规定条件下可继续使用的年限。

2.1.8  安全等级    safety class

   根据工程结构破坏所产生后果的严重性划分的具有不同可靠度设置水平的设计等级。

2.1.9  设计状况  design situation

   代表一定时段内实际情况的一组设计条件，设计应做到在该组条件下结构不超越有关的极限状态。

2.1.10  极限状态  limit state

   结构或构件超过某一特定状态就不能满足设计规定的某一功能要求，此特定状态为该功能的极限状态。

2.1.11  极限状态方程    limit state equation

   结构或构件处于极限状态时，各有关基本变量的关系式。

2.1.12  承载能力极限状态    ultimate limit state

   结构或构件达到最大承载力或产生不适于继续承载的变形的状态。

2.1.13  正常使用极限状态    serviceability limit state

   结构或构件达到正常使用或耐久性能的某项规定限值的状态。

2.1.14  可逆正常使用极限状态    reversible serviceability limit state

   当产生超越正常使用要求的作用卸除后，该作用产生的超越状态可以恢复的正常使用极限状态。

2.1.15  不可逆正常使用极限状态    irreversible serviceability limit state

   当产生超越正常使用要求的作用卸除后，该作用产生的超越状态不可恢复的正常使用极限状态。

2.1.16  疲劳极限状态  fatigue limit state

   重复荷载作用导致结构或构件失效，不适于继续承载的极限状态。

2.1.17  结构重要性系数  importance factor of structure

   根据结构安全等级所规定的对作用效应附加的调整系数。

2.1.18  基本变量  basic variable

   代表物理量的一组规定的变量，用于表示作用和环境影响、材料和岩土的性能以及几何参数的特征。

2.1.19  功能函数  performance function

   关于基本变量的函数，该函数表征一种结构功能。

2.1.20  概率分布  probability distribution

   随机变量取值的统计规律，一般采用慨率密度函数或概率分布函数表示。

2.1.21  统计参数    statistical parameter

   在概率分布中用来表示随机变量取值的平均水平和离散程度等的数字特征。

2.1.22  分位值    fractile

   与随机变量概率分布函数的某一概率对应的值。

2.1.23  特征值    characteristic value

   用统计方法确定的一定保证率或跨阈率下的值。

2.1.24  名义值    nominal value

   用非统计方法确定的值。

2.1.25  校准法    calibration method

   通过对现存结构或构件安全储备的反演分析，确定设计采用的目标可靠指标的方法。

2.1.26  作用    action

   施加在结构上的集中力或分布力(直接作用，也称为荷载)和引起结构外加变形或约束变形的原因(间接作用)。

2.1.27  岩土作用  geotechnical action

   围岩、地基、坡体、地下水或地表水等传递到结构上的作用。

2.1.28  作用效应    effect of action

   作用引起的结构或构件的反应。

2.1.29  作用的标准值    characteristic value of an action

   作用的主要代表值，可根据对观测数据的统计、作用的自然界限或工程经验确定。

2.1.30  可变作用的组合值    combination value of a variable action

   使组合后的作用效应的超越概率与该作用单独出现时其标准值作用效应的超越概率趋于一致的作用值；或组合后使结构具有规定可靠指标的作用值。可通过组合值系数(ψc≤1)对作用标准值的折减来表示。

2.1.31  可变作用的频遇值    frequent value of a variable ac-tion

   在设计基准期内被超越的总时间占设计基准期的比率较小的作用值；或被超越的频率限制在规定频率内的作用值。可通过频遇值系数(ψf≤1)对作用标准值的折减来表示。

2.1.32  可变作用的准永久值    quasi-permanent value of a variable action

   在设计基准期内被超越的总时间占设计基准期的比率较大的作用值。可通过准永久值系数(ψq≤1)对作用标准值的折减来表示。

2.1.33  作用的代表值    representative value of an action

   极限状态设计所采用的作用值，它可以是作用的标准值、组合值、频遇值或准永久值。

2.1.34  作用的设计值  design value of an action

   作用代表值与作用分项系数的乘积。

2.1.35  作用组合(荷载组合)    combination of actions(load combination)

   结构或构件设计时，预计可能同时出现的几种不同作用(效应)的集合。

2.1.36  主导可变作用  leading variable action

   在同一作用组合中，作用效应设计值最不利情况下起控制作用的可变作用。

2.1.37  标准组合  characteristic combination

   正常使用极限状态设计时，采用永久作用标准值、主导可变作用的标准值和(或)非主导可变作用的组合值的组合。

2.1.38  频遇组合    frequent combination

   正常使用极限状态设计时，采用永久作用标准值、主导可变作用的频遇值和(或)非主导可变作用的准永久值的组合。

2.1.39  准永久组合  quasi-permanent combination

   正常使用极限状态设计时，采用永久作用的标准值和可变作用的准永久值的组合。

2.1.40  环境影响  environmental influence

   环境对结构产生的各种机械的、物理的、化学的或生物的不利影响。

2.1.41  抗力    resistance

   结构或构件承受作用效应的能力。

2.1.42  材料性能的标准值    characteristic value of a material property

   符合规定质量的材料性能概率分布的某一分位值或材料性能的名义值。

2.1.43  材料性能的设计值  design value of a material prop-erty

   材料性能的标准值除以材料性能分项系数所得的值。

2.1.44  几何参数的标准值  characteristic value of a geomet-rical parameter

   设计规定的几何参数公称值或几何参数概率分布的某一分位值。

2.1.45  几何参数的设计值  design value of a geometrical pa-rameter

   几何参数的标准值增加或减少一个几何参数的附加量所得的值。

2.1.46  限值    constraint value

   结构或构件设计时，作为极限状态标志的应力、变形等的约束值。

2.1.47  疲劳荷载谱  fatigue load spectrum

   反映结构设计使用年限内在指定列车运量条件下，在列车疲劳荷载作用下材料或连接的作用效应和频次的关系，可用表格或直方图表达。

2.1.48  等效等幅重复应力法    method of equivalent constant amplitude stress range

   结构或构件在疲劳检算中，根据线性累积损伤法则或其他适当方法，将变幅重复应力转换为等幅重复应力进行设计的方法。

2.1.49  极限损伤度法  cumulative damage method

   结构或构件在疲劳检算中，根据线性损伤理论，将累积损伤度作为检算内容的设计方法。

2.2.1 结构可靠度：

Pf——结构或构件失效概率的运算值；

R——结构或构件的抗力；

S——结构或构件的作用效应；

T——设计基准期；

wi——第i种结构的权系数；

Xi——第i个基本变量；

X*i——基本变量Xi在分位概率为Φ(βXi)处的分位值；

X*′i——基本变量Xi在分位概率为Φ(βXi)处的分位值导数；

Z——结构或构件的功能函数；

αXi——基本变量Xi的灵敏度系数；

β——结构或构件的可靠指标；

βXi——基本变量Xi的分项可靠指标；

σR——抗力的标准差；

σS——作用效应的标准差；

σXi——基本变量Xi的标准差。

2.2.2 作用和作用效应：

F——作用；

Fk——作用的标准值；

Fr——作用的代表值；

G——永久作用；

Gk——永久作用的标准值；

SGk——永久作用标准值的效应；

Q——可变作用；

Qk——可变作用的标准值；

Qr——可变作用的代表值；

SQk——可变作用标准值的效应；

ψc——可变作用的组合值系数；

ψf——可变作用的频遇值系数；

ψq——可变作用的准永久值系数；

ψcQk——可变作用的组合值；

ψfQk——可变作用的频遇值；

ψqQk——可变作用的准永久值。

2.2.3 材料性能和几何参数：

a——几何参数；

anom——几何参数的标准值或名义值；

f——结构材料性能；

fk——结构材料性能f的标准值；

δf——结构材料性能f的变异系数。

2.2.4 结构极限状态设计式：

ad——几何参数a的设计值；

Cd——设计对结构达到正常使用(如变形、裂缝等)所规定的相应限值；

Fd——作用F的设计值；

fd——材料性能f的设计值；

Gd——永久作用G的设计值；

Qd——可变作用Q的设计值；

Rd——结构抗力R的设计值；

Sd——作用效应的设计值；

AEk——地震作用的标准值；

βnom——结构的目标可靠指标；

γ0——结构重要性系数；

γⅠ——地震作用重要性系数；

γF——作用的分项系数；

γsd——计算模型不定性系数；

γm——材料或产品性能的分项系数；

γRd——抗力模型不定性系数；

γM——材料或产品性能的分项系数，考虑模型不定性和(或)几何参数偏差等影响；

γL——考虑结构设计使用年限的荷载调整系数；

γR——抗力分项系数；

γG——永久作用G的分项系数；

γQ——可变作用Q的分项系数；

△a——几何参数a的附加量。

2.2.5 结构疲劳极限状态验算式：

γfat——钢结构疲劳作用分项系数；

△σe——钢结构验算部位等效等幅重复应力幅标准值(计入运营动力系数、离心力)；

△σ0——钢结构验算部位疲劳设计强度；

△faek——钢结构验算部位材料(或构造细节)的等幅疲劳强度标准值；

γaf——钢结构验算部位材料(或构造细节)的疲劳抗力分项系数；

γcek、γpek、γsek——分别为混凝土、预应力钢筋、钢筋的疲劳作用分项系数；

γcf、γpf、γsf——分别为混凝土、预应力钢筋、钢筋的疲劳抗力分项系数；

σcek、△σpek、△σsek——分别为混凝土结构验算部位的混凝土等效疲劳应力标准值、预应力钢筋等效疲劳应力幅标准值、钢筋等效疲劳应力幅标准值(计入运营动力系数、离心力)；

fcek、△fpek、△fsek——分别为混凝土结构验算部位的混凝土、预应力钢筋、钢筋的等幅疲劳强度标准值。

3.1.1  铁路工程结构的设计、施工和维护应使其在设计使用年限内以规定的可靠度满足规定的各项功能要求。

▼ 展开条文说明
3.1.1  铁路工程结构可靠度与结构设计使用年限有关。对新建结构可靠度而言，本标准是指设计使用年限中要满足结构可靠度的最低要求，当结构的使用年限超过设计使用年限后，结构的失效概率可能较设计预期值增大。
在铁路工程结构全寿命周期中，安全可靠是首要任务，在安全的基础上还要考虑经济性。

3.1.2  铁路工程结构应达到规定的可靠性水平，并满足下列功能要求：

   1  承受在施工和使用期间可能出现的各种作用，即满足承载能力极限状态或疲劳极限状态要求；

   2  保持良好的使用性能，并具有足够的耐久性能，即满足正常使用极限状态要求；

   3  发生洪水、非正常撞击、列车脱轨等偶然事件时，结构保持必要的整体稳固性，不出现与起因不相称的破坏后果；发生火灾时，在规定的时间内可保持足够的承载力。

▼ 展开条文说明
3.1.2  铁路工程结构在规定的可靠性水平下需要满足各种极限状态的要求：
1  本款目的是保证结构的安全性，对应结构的承载能力极限状态或疲劳极限状态，涉及强度、稳定和疲劳等。
2  本款针对正常使用极限状态而言，目的是保证结构的适用性和耐久性。适用性包括结构变形、旅客乘坐舒适度、列车运行平稳性等。结构耐久性是指结构在规定工作环境下，在预定时期内，不致因材料性能的劣化(如混凝土腐蚀或钢筋锈蚀)而影响结构的使用寿命；从工程慨念上讲，耐久性是指结构在正常维护条件下能够正常使用到规定设计使用年限的性能要求。
3  在发生偶然事件状况下，结构要保证其整体稳固性，偶然事件包括洪水、爆炸(铁路附近的工厂爆炸、恐怖袭击等)、非正常撞击、列车脱轨、地震等偶然作用导致的突发事件。所渭整体稳固性，系指在偶然事件发生时和发生后，工程结构仅产生局部的损坏、缺损而不致发生连续倒塌而危及使用者的生命，即使破坏倒塌也有明显的预兆或者发展过程，使有关人员有逃离现场的可能。
由于偶然事件往往产生特大的作用力，一般说来，要求结构仍保持完整无损是不现实的，只能要求结构不致因此而造成与其起因不相称的破坏后果。如当发生火灾时，结构能在一段时间内保持承载能力。对于这些偶然事件，设计者要采取必要的措施，避免无预兆的脆性破坏以及因局部破坏而引发的结构解体和连续倒塌。

3.1.3  铁路工程结构设计时，应选择适宜的计算模型和合理的基本变量值，并按下列要求采取适当措施：

   1  应避免、消除或减少结构可能受到的危害；

   2  应采用对可能受到的危害反应不敏感的结构类型；

   3  应采用当单个构件或结构的有限部分被意外移除或结构出现可接受的局部破坏时，结构其他部分仍能保存的结构类型；

   4  不宜采用无破坏预兆的结构体系。

3.1.4  铁路工程结构的勘察设计、施工、使用与维护等应采取相应的可靠性管理措施。

▼ 展开条文说明
3.1.3、3.1.4  工程结构的安全性和可靠性是一个广义概念，涉及结构从设计、制造、施工到投入使用，再到使用若干年后结构性能逐步退化的整个时间历程，是一个全寿命周期。结构全寿命过程不同阶段相互联系，互为因果，存在相辅相成的关系，共同保证结构的可靠性。
国外分析了150个钢结构失效案例，发现29.5％的原因在于施工架设阶段；26.7％的原因在于工程设计或工厂记录错误；14.3％的原因在于运营使用阶段，如超载之类；12.4％的原因在于制造阶段；10.5％的原因在于钢材质量不合格；6.6％的原因在于标准或技术条件不完善。可见，结构全寿命周期任一环节出现问题就可能造成严重后果。为从根本上保证工程结构在设计使用年限内的安全性、适用性和耐久性，对结构勘察设计、施工、使用与维护等方面提出要求和规定。
随着服役年限的增长，材料性能的劣化可能会导致既有结构抗力的降低，而承受的作用效应可能会增加，必要时应进行可靠性评定以获取既有结构的安全度水平，为维修养护决策提供依据。

3.2.1  铁路工程结构的设计根据结构破坏可能产生后果的严重程度，应采用表3.2.1规定的安全等级。

表3.2.1  铁路工程结构的安全等级

▼ 展开条文说明
3.2.1  本条为强制性条文，必须严格执行。在本标准中，按结构破坏可能产生后果的严重性统一划分为三个安全等级。其中，一般结构安全等级为二级(不以高速铁路、普速铁路等为划分依据)，特别重要的结构提高一级，次要的结构降低一级，至于安全等级的划分则根据工程结构的破坏后果即危及人的生命、造成经济损失、产生社会和环境影响等的严重程度确定。

3.2.2  铁路工程结构安全等级应按表3.2.2的规定划分。

表3.2.2  铁路工程结构安全等级划分

   注：对于有特殊要求的铁路工程结构，其设计安全等级可根据具体情况确定。

▼ 展开条文说明
3.2.2  根据结构破坏后果严重性的不同，将桥梁、隧道、路基和轨道不同结构类型划分到三个安全等级中。其中大部分工程结构安全等级为二级。对于有特殊要求的铁路工程结构，依据实际情况，其设计安全等级可根据具体情况确定。其中水下隧道主要指跨江、跨海或跨河的隧道。

3.2.3  铁路工程结构各类构件的安全等级宜与结构的安全等级相同，必要时可对部分构件的安全等级进行调整。

▼ 展开条文说明
3.2.3  铁路工程结构各类构件一般与结构采用相同的安全等级，但允许部分构件根据其重要程度和综合经济效果进行调整。如提高某一构件的安全等级所需额外费用很少，却能降低整个结构的破坏慨率，从而大大减少人员伤亡和财物损失，则可将该构件的安全等级相比整个结构安全等级进行提高；相反，如某一构件的失效并不影响整个结构或其他构件的安全，则可将其安全等级降低。

3.2.4  可靠性水平的设置应根据结构或构件的安全等级、失效模式和经济因素等确定。

3.2.5  有充分的统计数据时，结构或构件的可靠性宜采用可靠指标β度量。结构或构件设计采用的可靠指标，可根据对现有结构或构件的可靠度分析，并结合使用经验和经济因素等确定。

▼ 展开条文说明
3.2.5  对有充分统计数据的结构或构件，其可靠性大小宜采用可靠指标β度量与比较。

3.2.6  铁路工程结构的破坏类型可分为延性破坏和脆性破坏，其中脆性破坏的可靠度应高于延性破坏的可靠度。

▼ 展开条文说明
3.2.6  脆性破坏和延性破坏，又称为无预兆破坏和有预兆破坏，为避免无预兆破坏带来的突发性损失，规定脆性破坏可靠度要高于延性破坏可靠度。铁路工程结构的脆性破坏，主要指混凝土及预应力混凝土结构强度破坏、钢结构或混凝土结构剪切破坏、结构整体或局部失稳破坏、钢结构脆性断裂等；疲劳破坏属于特殊的脆性断裂破坏。岩土工程的破坏形式主要可分为整体剪切破坏、局部剪切破坏和冲剪破坏，也可归于脆性或延性破坏的范畴。

3.3.1  铁路工程结构设计时，应规定结构的设计使用年限。

▼ 展开条文说明
3.3.1  本条为强制性条文，必须严格执行。设计文件中应规定结构的设计使用年限，而无需标明结构的设计基准期、耐久年限、寿命等。设计使用年限确定的原则可结合预期使用寿命、确定设计参数取值的基准期和已有应用经验。

3.3.2  铁路工程结构设计使用年限应按100年、60年和30年分级。

▼ 展开条文说明
3.3.2  本条明确了铁路桥涵、隧道、路基和轨道结构设计使用年限的三个级别，这不仅是进行可靠性设计的基础，也是保证结构设计经济合理的必要环节。
表2中列举了不同设计使用年限级别的适用范围示例，供设计人员参考。
           表2  铁路工程结构设计使用年限示例

3.3.3  铁路工程结构设计应考虑环境影响，根据不同环境类别采用相应的结构材料、设计构造、防护措施、施工质量要求等，制定结构在使用期间的定期检修和维护制度，使结构在设计使用年限内满足安全和正常使用的要求。

3.3.4  环境对铁路工程结构耐久性的影响，可通过工程经验、试验研究、理论计算或综合分析等方法进行评估。

3.3.5  环境类别的划分和相应的设计、施工、使用及维护的要求等，应符合国家现行有关标准的规定。

▼ 展开条文说明
3.3.3～3.3.5  我国部分工程结构存在严重的耐久性问题，究其原因，不外乎是设计考虑不周、施工水平不高(缺陷)和养护维修不到位等。除此之外，环境是影响结构耐久性的主要因素之一。外界环境和结构设计、施工的自身缺陷共同作用，加速了结构劣化进程，降低了结构使用寿命，使结构不得不提前进行维修加固。因此，本标准强调结构的耐久性设计，重视环境对结构耐久性的影响，这是可靠性设计的重要内容。
同类结构物的不同部位所处的环境类别和作用等级往往有所差别，其耐久性要求也有所不同，甚至同一构件的不同部位，其耐久性要求差别也可能很大，这就要求不同的环境类别采取相应措施，并制定检修和维护制度以保证耐久性。
由于对环境影响效果予以量化较为困难，因此在评估环境对铁路工程结构耐久性影响时，一般是采用工程经验、试验研究、理论计算或综合分析等方法。

4.1.1  铁路工程结构应按承载能力极限状态和正常使用极限状态进行设计。承受重复荷载作用的构件尚应按疲劳极限状态进行检算。

4.1.2  结构或构件出现下列状态之一时，应认为超过了承载能力极限状态：

   1  结构、构件或连接超过材料强度，或过度变形不适于继续承载；

   2  结构或结构一部分作为刚体失去平衡；

   3  结构体系成为机动体系；

   4  结构或构件失稳；

   5  地基失去承载能力；

   6  影响结构安全的其他特定状态。

4.1.3  结构或构件出现下列状态之一时，应认为超过了正常使用极限状态：

   1  影响正常使用的变形；

   2  影响正常使用或耐久性能的裂缝、局部损坏；

   3  影响正常使用和舒适性的振动；

   4  影响正常使用的其他特定状态。

4.1.4  结构或构件在重复荷载累积损伤作用下出现下列状态之一时，应认为超过了疲劳极限状态：

   1  影响安全使用的疲劳裂纹；

   2  影响安全使用的变形。

▼ 展开条文说明
4.1.1～4.1.4  承载能力极限状态理解为结构或构件发挥允许的最大承载功能的状态。结构或构件由于塑性变形而使其几何形状发生显著改变，虽未达到最大承载能力，但已彻底不能使用，也属于达到这种极限状态。
正常使用极限状态理解为结构或构件达到使用功能上允许的某个限值的状态。正常使用极限状态的控制，往往需要采用一定的约束条件，例如，某些构件需控制变形、裂缝才能满足使用要求。因过大的变形会造成列车运行的平稳性下降，舒适度降低等后果，过大的裂缝会影响结构的耐久性；过大的变形、裂缝也会造成用户心理上的不安全感，这些约束条件一般以规定值的形式列入规范。
疲劳是在循环拉应力或拉压应力作用下，在应力集中或缺陷处引发疲劳裂纹，发展到最后会导致结构或构件破坏，该状态为疲劳极限状态。疲劳对直接承受列车荷载的轨道结构以及承受重复荷载动力作用的桥梁结构等影响较大，特别是目前桥梁钢结构的连接多采用焊接，焊接会引入焊接缺陷，容易诱发疲劳裂纹；部分结构由于环境影响加快了疲劳裂纹的扩展而导致严重后果，如1967年12月15日服役近40年美国的银桥(Silver Bridge)突然整桥倒塌，造成46人丧生，事故调查原因是眼杆销孔处两条腐蚀疲劳裂纹导致C13号结合处发生脆断引起整座桥的倒塌。
基于疲劳极限状态与承载能力极限状态在作用形式(以拉为主的重复荷载作用)，抗力(与构造细节高度相关，材料强度不是控制因素)，计算模型(实验科学，无明确的力学模型)等方面的不同，同时考虑部分铁路工程结构中列车重复荷载作用是主导作用，因此，疲劳极限状态单独列举出来有其必要性。
美国AASHTO规范和日本铁路混凝土等规范都将疲劳极限状态单独划分为一种极限状态，欧洲规范Eurocode虽将疲劳极限状态归为承载能力极限状态中，但很多条款是单独针对疲劳极限状态规定的。
因此，本次修订细化了极限状态的分类，将疲劳极限状态与承载能力极限状态和正常使用极限状态并行，构成铁路工程结构的三种极限状态。

4.1.5  铁路工程结构设计应规定各种极限状态的标志或限值。

▼ 展开条文说明
4.1.5  设计限值是结构或构件按极限状态设计时，采用的作为极限状态标志的应力或变形等的界限值。
极限状态的标志及限值是根据对结构各种功能失效的机理研究后制定的。当失效机理研究不充分时，为满足工程设计需要，可以根据理论研究成果结合工程经验判断或按现行规范确定。如破坏的强度准则，就是结构到达承载能力极限状态的标志之一；裂缝宽度、振动响应等造成用户心理上的不安全感时，就是结构到达正常使用极限状态的标志之一。

4.1.6  铁路工程结构或构件设计应对不同极限状态进行计算或验算，并确保结构构造合理。

▼ 展开条文说明
4.1.6  铁路工程结构或构件设计要满足承载能力极限状态、正常使用极限状态和疲劳极限状态要求，对这些极限状态进行计算或验算，确定起控制作用的极限状态。
在三种极限状态都满足的情况下，为保证结构或构件的耐久性，合理设计和布置结构细部构造非常必要。经过多年实践证明，结构细部构造的设计不合理是导致病害发生的主要原因。因此，要从设计源头上保证结构构造合理。

4.1.7  铁路工程结构极限状态可采用以作用效应和抗力等组成的极限状态方程表达。

▼ 展开条文说明
4.1.7  铁路工程结构极限状态是通过各种基本变量组成的极限状态方程来实现，基本变量是指极限状态方程中所包含的影响结构可靠度的各种物理量，包括引起结构作用效应上的各种作用S，如恒荷载、活荷载、地震、温度变化等，结构抗力R的各种因素如材料性能、几何参数等。分析时，可将作用效应或结构抗力作为综合基本变量考虑。无特殊说明时，基本变量一般可视为相互独立的随机变量。

4.2.1  铁路工程结构设计应考虑下列设计状况：

   1  持久设计状况，适用于结构使用时的正常情况，应考虑在设计基准期内承受的永久作用、列车作用、土压力、风、温度等相对持续时间长的作用；

   2  短暂设计状况，适用于结构施工、运营、维修时承受的临时性或短暂情况，应考虑恒载、施工人员和施工机具、运架设备等作用；

   3  偶然设计状况，适用于结构使用的异常情况，应考虑火灾、撞击、脱轨、断轨、落石冲击等作用；

   4  地震设计状况，适用于结构遭受地震时的情况，应考虑结构在地震作用下的受力分析和结构验算。

▼ 展开条文说明
4.2.1  原国家标准《铁路工程结构可靠度设计统一标准》GB 50216-94规定铁路工程结构设计时考虑了持久设计状况(含疲劳作用)、短暂设计状况和偶然设计状况三种设计状况，本标准增加了地震设计状况。这主要由于地震作用具有与火灾、爆炸、撞击或局部破坏等偶然作用不同的特点：首先，我国很多地区处于地震设防区，需要进行抗震设计且很多结构是由抗震设计控制的。其次，地震作用是能够统计并有统计资料的，可以根据地震的重现期确定地震作用。最后，现行国家标准《铁路工程抗震设计规范》GB 50111对地震设计做出了详细规定，因此，本次修订在三种设计状况的基础上，借鉴欧洲规范EN 1990：2002和现行国家标准《工程结构可靠性设计统一标准》GB 50153的规定，增加了地震设计状况。
地震作用依据重现期不同分为多遇地震、设计地震和罕遇地震，重现期即是连续两次超过某一规定值的平均时间间隔。

4.2.2  铁路工程结构设计应根据每种设计状况采用相应的结构体系、可靠性水平、基本变量和作用组合等。

4.3.1  不同设计状况条件下，铁路工程结构设计应符合下列规定：

   1  对持久设计状况，应进行承载能力和正常使用极限状态设计，必要时进行疲劳极限状态检算；

   2  对短暂设计状况，应进行承载能力极限状态设计，可根据需要进行正常使用极限状态设计；

   3  对偶然设计状况，应进行承载能力极限状态设计；

   4  对地震设计状况，应进行承载能力极限状态设计，可根据工程需要进行正常使用极限状态设计。

▼ 展开条文说明
4.3.1  持久设计状况是贯穿结构全寿命周期的设计情况，要满足承载能力极限状态和正常使用极限状态的要求；承受重复荷载作用的构件或构造细节，还应考虑疲劳极限状态。
短暂状况在结构施工和使用过程中一定出现，根据性能要求不同考虑承载能力极限状态和正常使用极限状态。
偶然状况主要涉及偶然事件，只进行承载能力极限状态验算，主要承载结构应采用下列原则之一进行设计：
(1)按作用效应的偶然组合进行设计或采取保护措施，使主要承载结构不致因偶然事件而丧失承载能力。
(2)允许主要承载结构因偶然事件而局部破坏，但结构的剩余部分仍应具有在一段时间内不发生继发性破坏的可靠性。
地震状况按承载能力极限状态进行设计，使主要承载结构不致因出现设计的地震状况而丧失承载力；按照多遇地震设计的工程结构，还需要满足正常使用极限状态要求。

4.3.2  铁路工程结构承载能力极限状态设计，可根据不同的设计状况采用下列作用组合：

   1  基本组合，用于持久设计状况或短暂设计状况；

   2  偶然组合，用于偶然设计状况；

   3  地震组合，用于地震设计状况。

4.3.3  铁路工程结构正常使用极限状态设计，可根据具体情况采用下列组合：

   1  标准组合，宜用于不可逆正常使用极限状态设计；

   2  频遇组合，宜用于可逆正常使用极限状态设计；

   3  准永久组合，宜用于长期效应为决定性因素的正常使用极限状态设计。

▼ 展开条文说明
4.3.2、4.3.3  承载能力极限状态的荷载组合有基本组合、偶然组合和地震组合，分别对应持久设计和短暂设计状况、偶然设计状况和地震设计状况。当考虑偶然事件产生的作用(如列车脱轨)时，此时采用的结构可靠指标适当降低。
正常使用极限状态分为不可逆极限状态和可逆极限状态，荷载组合有标准组合、频遇组合和准永久组合。
标准组合用于不可逆正常使用极限状态，当超越极限状态时将产生永久性不可逆损坏。如有抗裂要求的构件，一旦产生裂缝会造成不可逆的损坏。
频遇组合用于可逆正常使用极限状态，如构件的变形、振动等情况。
准永久组合用于当长期效应为决定性因素的正常使用极限状态设计。

4.3.4  铁路工程结构设计应满足各种极限状态下最不利作用组合的要求。

4.3.5  铁路工程结构极限状态设计应符合下式规定：

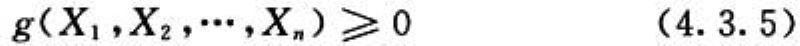
   式中：    g(·)——结构的功能函数；

          Xi(i＝1，2，…，n)——基本变量。在进行可靠性分析时，基本变量应作为随机变量。

4.3.6  结构功能函数将作用效应和结构抗力作为综合基本变量时，结构极限状态设计应符合下式规定：

   式中：R——结构的抗力；

         S——结构的作用效应。

▼ 展开条文说明
4.3.5、4.3.6  极限状态方程是当结构处于极限状态时各有关基本变量的关系式。当结构设计问题中仅包含两个基本变量时，在以基本变量为坐标的平面上，极限状态方程为直线(线性问题)或曲线(非线性问题)；当结构设计问题中包含多个基本变量时，在以基本变量为坐标的空间中，极限状态方程为平面(线性问题)或曲面(非线性问题)。
功能函数g(R，S)描述结构某一功能所处的状态，g(R，S)＞0表示结构处于可靠状态；g(R，S)＝0表示结构处于极限状态；g(R，S)＜0表示结构处于失效状态；计算结构可靠度就是计算功能函数g(R，S)＞0的概率。
结构极限状态方程中的基本变量包括作用、环境影响、材料和岩土性能、结构几何参数、计算模式不定性等随机变量。若将结构设计问题中基本变量归结为抗力和作用项，进行极限状态设计即要求抗力不小于作用，即g(R，S)≥0。
结构功能函数中主要基本变量可用设计基准期内概率分布函数的最大值(最小值)随机变量描述，其他基本变量可用任意时点分布函数的随机变量描述。

4.3.7  铁路工程结构失效概率可按式(4.3.7-1)确定，也可根据结构可靠指标β按式(4.3.7-2)计算。

   式中：Φ(·)——标准正态分布函数。

▼ 展开条文说明
4.3.7  为了统一我国铁路工程结构可靠性设计标准的基本原则，促进结构设计理论的发展，本标准采用了以概率理论为基础的极限状态设计方法。
以往采用的半概率极限状态设计方法，仅在荷载和材料强度的设计取值上考虑了各自的统计变异性，没有对结构或构件的可靠度给出科学的定量描述。这种方法常常使人误认为只要设计中采用了某一给定安全系数，结构就能百分之百的可靠，将设计安全系数与结构可靠度简单地进行等同。而以概率理论为基础的极限状态设计方法则是以结构失效概率来定义结构可靠度，并以与结构失效概率Pf相对应的可靠指标β来度量结构可靠度，从而能较好地反映结构可靠度的实质，使设计概念更为科学和明确。
表3为可靠指标β与失效概率Pf的对应关系。
               表3  可靠指标β与失效概率P_f对照表

表3中可靠指标β与失效概率P_f的对应关系是在功能函数服从正态分布情况下而来，当功能函数不服从正态分布时，要先转化为正态分布再进行计算。

4.3.8  根据铁路工程结构极限状态方程和随机变量的特征，可选用本标准附录A.1的一次二阶矩法(分位值法、JC法)、蒙特卡罗法或其他适宜方法计算可靠指标。

▼ 展开条文说明
4.3.8  根据极限状态方程是否为线性方程以及综合基本变量R和S概率分布的不同，根据《铁路工程结构极限状态设计通用方法及专业参数处理分析研究》[合同编号：铁建科字(2009)-2)]的科研成果，推荐了计算可靠指标的JC法，JC法也是国际结构安全度联合委员会(JCSS)推荐的方法。分位值法是原国家《铁路工程结构可靠度设计统一标准》GB 50216-94中推荐使用的方法。JC法和分位值法都属于一次二阶矩法，两者皆能考虑非正态随机变量，岩土工程领域采用蒙特卡罗法相对较多，因此本标准推荐JC法、分位值法、蒙特卡罗法计算可靠指标，根据具体情况不同，可靠指标的计算也可选用数值积分法、响应面法等其他方法。

4.3.9  铁路工程结构或构件的可靠指标，不应小于规定的目标可靠指标。目标可靠指标可按本标准附录A.2的校准法为基础确定。

▼ 展开条文说明
4.3.9  铁路工程结构设计要保证结构的计算可靠指标不小于目标可靠指标，只有这样，才能保证结构在设计使用年限的安全性和可靠性，即目标可靠指标与设计使用年限是紧密相关的。根据规范科研《铁路工程结构目标可靠指标制定研究》(专项编制2012-02)的研究成果，给出了铁路工程结构极限状态法转轨时目标可靠指标的参考：
(1)桥梁结构目标可靠度指标建议值：承载能力极限状态，按结构安全等级不同，延性破坏为4.2、4.7、5.2，脆性破坏为4.7、5.2、5.7；正常使用极限状态为1.5～3.0。
(2)铁路隧道二次衬砌、明洞目标可靠度指标建议值：承载能力极限状态，按结构安全等级不同，延性破坏为3.2、3.7、4.2，脆性破坏为3.7、4.2、4.7；正常使用极限状态为1.0～2.5。
(3)铁路路基目标可靠度指标建议值：承载能力极限状态，抗滑、倾覆和地基应力按结构安全等级不同分为2.7、3.2、3.7；正常使用极限状态为1.0～2.5。
(4)轨道目标可靠度指标建议值：承载能力极限状态，按结构安全等级不同，延性破坏为3.2、3.7、4.2，脆性破坏为3.7、4.2、4.7；正常使用极限状态为1.0～2.5。

4.3.10  铁路工程结构或构件承载能力极限状态的目标可靠指标应按安全等级进行分级。每相差一级，目标可靠指标的差值宜取0.5，也可经综合分析确定。

▼ 展开条文说明
4.3.10  针对承载能力极限状态，不同安全等级和失效模式的可靠指标要适当拉开档次。国外计算分析表明，由于重要性系数取值不同，相邻安全等级的结构或构件可靠指标有0.5的级差，基于此，参照国内外目标可靠指标的分级，规定安全等级每相差一级，可靠指标取值宜相差0.5，安全等级相同，脆性破坏结构或构件的设计可靠指标与延性破坏相差0.5。当然，也可以根据实际综合分析确定。

4.3.11  铁路工程结构或构件宜根据规定的目标可靠指标，采用由作用的代表值、材料性能的标准值、几何参数的标准值和各相应分项系数构成的极限状态设计表达式进行设计，分项系数宜按本标准附录A.3的方法确定。

▼ 展开条文说明
4.3.11  为照顾原有设计习惯，结构可靠性设计是通过多个分项系数组成的表达式来实现，而分项系数的获取则是通过结构的计算可靠指标与目标可靠指标最佳一致性优化而定。
概率极限状态设计式中的分项系数不同于多系数极限状态设计法中的分项系数，前者是通过统计分析优化而得，后者是简单地将单一安全系数K分解为多个系数，没有涉及结构的可靠性。当统计资料足够多或者社会生产技术条件发生大的飞跃时，可以适当调整分项系数，体现概率极限状态设计法的生命力。

4.4.1  铁路工程结构有条件时可直接采用基于可靠指标方法进行设计。

4.4.2  铁路工程直接采用基于可靠指标方法进行设计时，所设计结构或构件的计算可靠指标应满足下式要求：

   式中：β——所设计结构或构件的可靠指标；

         βnom——所设计结构或构件的目标可靠指标。

▼ 展开条文说明
4.4.1、4.4.2  基于可靠指标的设计是以分项系数表达的极限状态设计方法的进一步发展，又称概率设计法，该法是使所设计结构的可靠性满足某个规定的概率度量值，即失效概率在某一时期内不超过某个规定值。主要应用于：①直接设计某些重要的工程，使其获得接近规定的可靠性；②对不同设计状况下的结构可靠性进行一致性对比；③按规定可靠性进行设计参数校准。

4.4.3  按可靠指标方法与传统方法设计的结果有明显差异时，应分析原因；只有当证明可靠指标方法设计结果合理后方可采用。

▼ 展开条文说明
4.4.3  直接用可靠指标方法对结构或构件进行设计，理论上是科学的，但目前由于数据统计资料尚未全面，暂不具备进行基于可靠指标的设计条件。因此，如果用可靠指标方法设计的结果与按传统设计的结果存在差异，并不能说明哪种方法结果一定是合理的，而要根据具体情况进行分析。

5.1.1  铁路工程结构上的作用按随时间上的变化，可分为永久作用、可变作用和偶然作用。桥涵、隧道、路基、轨道结构设计应根据具体特点规定相应的作用。

▼ 展开条文说明
5.1.1  根据作用随时间的变化，铁路工程结构的作用分为永久作用、可变作用和偶然作用，不同的作用应用于不同的作用组合。三种作用的分类如下：
永久作用的特点是其统计规律与时间参数无关，或者作用随时间而变异的量值与平均值相比可以忽略不计，永久作用包括：①结构自重；②结构附加恒载(线路设备及人行道等)；③预加应力；④混凝土收缩和徐变、钢材焊接变形作用；⑤土压力；⑥静水压力及浮力；⑦支座沉降、地基沉降作用；⑧结构施工变形作用；⑨其他永久作用。
可变作用的统计规律与时间参数有关，且变化值与平均值相比不能忽略不计的作用，包括：①列车活荷载(及动力系数)及其他可移动荷载；②长钢轨作用力(挠曲力、伸缩力)；③列车离心力；④列车横向摇摆力；⑤列车活载产生的土压力；⑥人行道人行荷载；⑦列车气动力；⑧列车制动力或牵引力；⑨风荷载；⑩支座摩阻力；

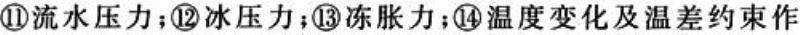
偶然作用在设计使用年限内不一定出现，而一旦出现其量值很大，且持续时间很短，包括：①列车脱轨荷载；②船舶或排筏撞击力；③汽车撞击力；④长钢轨断轨力；⑤落石冲击作用；⑥地震作用；⑦其他偶然作用。
由于桥涵、隧道、路基和轨道结构特点的不同，导致同种作用在不同结构中的归类可能不同。因此，桥涵、隧道、路基、轨道设计规范要根据具体特点确定相应作用，本标准不做统一规定。

5.1.2  结构上的各种作用在时间和空间上相互独立时，每一种作用可分别作为单个作用；某些作用密切相关且有可能同时以最大值出现时，可将这些作用一起作为单个作用。

▼ 展开条文说明
5.1.2  某些作用密切相关且有可能同时以最大值出现时，可视为单个作用，按一组主导作用进行效应的计算或组合。

5.1.3  铁路工程结构极限状态设计应根据结构特性和在结构上可能同时出现的作用，取最不利作用组合进行设计。组合值系数宜按本标准附录A.4的方法确定。

5.1.4  铁路工程结构设计应考虑结构上可能出现的各种作用和环境影响。

5.2.1  铁路工程结构上的作用随时间的变化规律宜采用随机过程概率模型描述，并应符合下列规定：

   1  对永久作用，在结构可靠性设计中可采用随机变量的概率模型。

   2  对可变作用，在作用组合中可采用简化的随机过程概率模型。在确定可变作用的代表值时可采用将设计基准期内最大值(或最小值)作为随机变量的概率模型。

   3  作用概率分布模型及其参数应根据适量的实际观测或试验检验数据统计分析确定。

▼ 展开条文说明
5.2.1  作为基本变量的作用，应尽可能根据它随时间变化的规律，采用随机过程的概率模型来描述。
永久作用的统计参数与时间基本无关，其随机性通常表现在随空间变异上，故可采用随机变量概率模型来描述。
可变作用的统计参数一般与时间参数有关，宜用随机过程概率模型来描述。在实用上可将随机过程概率模型转化为随机变量概率模型。
作用随机过程的样本函数十分复杂，它随荷载的种类不同而异。对于常见的风雪荷载等，为了简化，采用了平稳两项随机过程概率模型，即将它们的样本函数统一模型化为等时段矩形波函数，矩形波幅值的变化规律采用作用随机过程{Q(t)，t∈[0，T]}中任意时点作用的概率分布函数F_Q(x)＝P{Q(t₀)≤x，t₀∈[0，T]}来描述。
当采用基于概率论的极限状态设计法时，必须将作用随机过程转化为设计基准期的最大荷载：

因为T已规定，所以Q_T是一个与时间参数t无关的随机变量。因此常将可变作用在设计基准期内的极大值或极小值(当作用减小为不利时)作为随机变量来处理。
任意时点作用的概率分布函数是结构可靠性分析的基础。根据所获得的资料和数据进行统计分析，运用X²检验或K—S检验等方法，选择典型的概率分布如正态、对数正态、伽马、极值Ⅰ型、极值Ⅱ型、极值Ⅲ型等来拟合，检验的显著性水平可统一取0.05。
作用的统计参数，如平均值、标准差、变异系数等，要根据实测数据，按数理统计中参数估计方法确定。当统计资料不足、一时又难以获得时，需根据工程经验经适当的判断确定。

5.2.2  铁路工程结构设计在不同作用组合下应采用相应的作用代表值。永久作用应采用标准值作为唯一代表值，永久作用的标准值和概率分布可按本标准附录B.1的方法确定。可变作用应采用标准值、组合值、频遇值和准永久值作为代表值。

▼ 展开条文说明
5.2.2  任何作用都具有不同性质的变异性，但在工程设计中，不可能直接引用反映其变异性的各种统计参数并通过复杂的概率运算进行设计。因此，除了采用能便于设计者使用的分项系数设计表达式外，对作用仍要赋予一个规定的量值，称为作用的代表值。
根据设计的不同要求，可以规定不同的代表值，以便能更确切地反映它在设计中的特点。对可变作用而言，其代表值包括标准值、组合值、频遇值和准永久值。标准值是作用的基本代表值，而其他代表值都是在标准值的基础上乘以相应的折减系数来表示。

5.2.3  可变作用的标准值可采用其设计基准期或设计状况持续期内极大值(或极小值)概率分布的某一分位值。作用的增大对结构不利时，可取其极大值概率分布的某一高分位值；作用的减小对结构不利时，可取其极小值概率分布的某一低分位值；观测数据不充分时，可变作用的标准值也可根据工程经验通过分析判断确定。可变作用的概率分布和准永久值、频遇值及组合值可按本标准附录B.2的方法确定。

▼ 展开条文说明
5.2.3  根据概率极限状态设计方法的要求，可变作用的标准值可以取作用在设计基准期内极大值(或极小值)的概率分布的某一分位值。必要时作用的标准值也可以取有关规范规定的名义值或由工程经验确定。

5.2.4  对偶然作用，应采用偶然作用的设计值。偶然作用的设计值应根据有关标准确定，也可根据观测和试验数据以及工程经验综合分析确定。

▼ 展开条文说明
5.2.4  偶然作用是指在设计使用年限内不一定出现，而一旦出现其量值很大，且持续期在多数情况下很短的作用。因此偶然作用的出现是一种意外事件，其代表值即是设计值，应根据具体的工程情况和偶然作用可能出现的最大值，并且考虑经济上的因素综合确定，也可通过有关标准规定；若偶然作用有一定统计规律，其设计值也可以通过某一分位值来确定。

5.2.5  对地震作用，应采用地震作用的标准值。地震作用的标准值应根据地震作用的重现期确定。

▼ 展开条文说明
5.2.5  地震作用的代表值相当于设计基准期为50年超越概率为10％。如果采用重现期表示，基本烈度相当于重现期为475年地震烈度。我国规范将抗震设防划分为三个水准，第一水准是低于基本烈度，俗称小震，相当于50年超越概率为63.2％；第二水准是基本烈度；第三水准是罕遇地震烈度，俗称大震，相当于50年超越概率为2％，或重现期为2475年地震烈度。

5.2.6  铁路工程结构上的作用效应采用作用的函数式表达时，应根据试验、计算或经验确定其计算模型不定性系数。

▼ 展开条文说明
5.2.6  结构对于所受作用的反应称为作用效应。它可以是构件的轴力、弯矩和扭矩等，也可以是结构某一部位的裂缝宽度和变位等。
结构的作用效应与作用的关系，通过试验或计算确定。当作用与作用效应呈线性关系时，其比值称为作用效应系数；当作用与作用效应呈非线性关系时，作用效应采取作用的函数式表示。有些情况下，作用效应可以通过直接测定来获取，如混凝土轨下和轨中弯矩、钢轨的应力等。
按照极限状态设计方法，在许多情况下，需要采取作用效应为极限状态表达式的基本参数，这需要通过一定的换算关系由结构的作用求得，此时作用效应采用作用的函数式表达，应根据试验、计算或经验确定其模型不定性。

5.3.1  铁路列车竖向作用标准值应根据线路类型按表5.3.1确定。

表5.3.1  铁路列车荷载图式

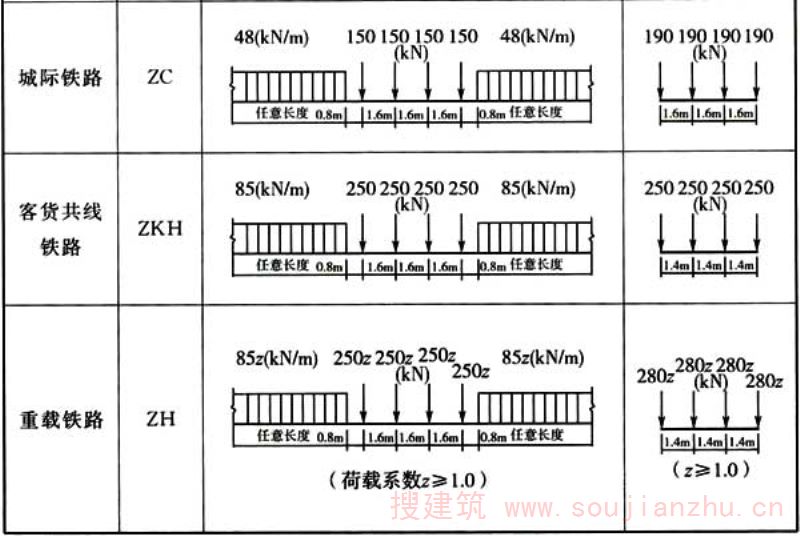
▼ 展开条文说明
5.3.1  铁路列车竖向作用是铁路工程结构承受的主要可变作用。目前现行行业标准《铁路列车荷载图式》TB／T 3466-2016已发布，本条与该标准一致。

5.3.2  有通过长大车辆要求的铁路工程结构，除应按本标准表5.3.1规定的作用进行设计外，尚应按长大重车检算图式(如图5.3.2所示)进行检算。

图5.3.2  长大重车检算图式

5.3.3  铁路列车竖向作用效应标准值，应在考虑动力效应基础上，按铁路列车荷载图式在结构验算部位最不利情况加载确定。

▼ 展开条文说明
5.3.3  在考虑动力效应基础上，根据列车荷载图式，计算作用在结构验算部位最不利位置产生的作用效应即为铁路列车作用效应标准值。

5.3.4  铁路列车作用效应概率分布可按本标准附录B.3的方法确定。

5.4.1  铁路工程结构设计，应在结构选材、材料规格、结构构件设计、构造要求中考虑环境对材料性能退化、结构耐久性降低等影响。

5.4.2  环境影响可用概率模型描述，也可采用单一环境对结构影响的分级描述，或若干环境影响的组合效应分级描述，并在设计中采取相应的技术措施。

▼ 展开条文说明
5.4.1、5.4.2  环境对铁路工程结构的影响多指酸雨腐蚀、混凝土碳化、盐侵蚀、钢材锈蚀等，加上外界温度、湿度的不断变化，会导致材料性能的降低，结构截面有效尺寸的减小，使结构抗力降低，影响结构的安全性、适用性和耐久性。
结构功能降低，不仅与材料本身有密切关系，同时一些细部构造设计往往未考虑服役环境的特殊要求，因此，铁路工程结构设计中应重视环境的影响。
环境影响在很多方面与作用相似，而且可以和作用相同地进行分类，特别是关于它们在时间上的变异性，因此，环境影响可分为永久、可变和偶然影响三类。例如，对处于海洋环境中的混凝土结构，氯离子对钢筋的腐蚀作用是永久影响，空气湿度对木材强度的影响是可变影响等。
如同作用一样，环境影响尽量采用定量描述。但在多数情况下，这样做是有困难的，因此，目前对环境影响只能根据材料特点，按其抗侵蚀性的程度来划分等级，设计时按等级采取相应措施。

6.1.1  材料性能宜采用随机变量概率模型描述。材料性能的统计参数和概率分布类型，应以实测或试验数据为基础，运用参数估计和概率分布的假设检验方法确定，检验的显著性水平α可取0.05。

▼ 展开条文说明
6.1.1  有些材料性能如土工合成材料、混凝土的强度等存在与时间变化相关的特性，但为了简化起见，各种材料性能仍作为与时间无关的随机变量来考虑，而性能随时间的变化一般通过引进换算系数来估计。当确定材料物理力学性能的标准值时，检验的显著性水平一般取0.05，对于小样本空间，显著性水平可适当增大。

6.1.2  材料强度随机变量的概率分布类型宜采用正态分布或对数正态分布。

6.1.3  材料物理力学性能的标准值应按规定的测试方法选取材料性能总体分布中的某一分位值确定，并宜符合下列规定：

   1  材料强度，宜取概率分布的0.05分位值；

   2  钢材疲劳强度，宜取概率分布的0.023分位值；

   3  材料弹性模量、泊松比等物理性能，宜取概率分布的0.5分位值；

   4  试验数据不足时，材料性能的标准值，可采用有关标准的规定值，也可根据工程经验，经分析判断确定。

▼ 展开条文说明
6.1.2、6.1.3  这两条规定了材料物理力学性能标准值的规定原则。
对材料而言，其强度的标准值是采用概率分布的低分位值，国际上一般取0.05，本标准也采用该分位值作为材料强度标准值。
正态分布可视为一种相对保守的分布，当从多个试验得到验证后，可采用对数正态等其他概率分布。

式中：μ_f、σ_f及δ_f分别为材料强度的平均值、标准差及变异系数。
钢材疲劳强度通常采用的是97.7％的保证率，即概率分布为0.023的分位值；钢筋疲劳强度通常采用的是95％的保证率，即概率分布为0.05的分位值。
对材料弹性模量、泊松比变异性较小的随机变量，取其平均值作为标准值，即概率分布的0.5分位值。
需要说明的是：试验数据不足时，材料性能的标准值可以采用有关标准的规定值，也可以根据工程经验，经分析判断确定。

6.1.4  材料性能可通过标准试件试验结果确定，试验应考虑下列情况：

   1  实际结构与标准试件、实际工作条件与标准试验条件的差别；

   2  实际结构与标准试件材料性能的关系，应考虑尺寸、时变、温度、湿度等影响因素，根据相应的对比试验结果通过换算系数或函数反映；

   3  结构中材料性能的不定性应考虑标准试件材料性能的不定性、换算系数或函数的不定性。

▼ 展开条文说明
6.1.4  用材料的标准试件试验所得的材料性能f_spe，一般不等同于结构中实际的材料性能f。例如，材料试件的加荷速度远超过实际结构的受荷速度，致使试件的材料强度较实际结构偏高；试件的尺寸远小于结构的尺寸，致使试件的材料强度受尺寸效应的影响而与结构本身不同；有些材料，如混凝土，其标准试件的成型、养护条件与实际结构并不完全相同，有时甚至相差很大，所有这些因素导致两者的材料性能有所差别。
一般习惯采用换算系数或函数K_str来考虑，从而结构中实际的材料性能与标准试件材料性能的关系按下式表示：

结构构件材料性能的平均值f和变异系数δ_f在综合考虑试件材料性能f_spe和材料性能换算系数K_str的概率分布参数的基础上，按下式确定：

式中：δ_f——结构材料性能f的变异系数；
     δf_spe——试件材料性能f_spe的变异系数；
     δK_str——材料性能换算系数K_str的变异系数。
由于结构所处的状态具有变异性，因此换算系数或函数K_str也是随机变量，有时可以简化为常量。

6.1.5  岩土性能宜根据试验结果采用随机变量概率模型来描述，也可采用多变量正态分布。岩土性能标准值应按下列方法确定：

   1  根据概率分布的某一分位值确定；

   2  试验数据不足、从有关标准或研究成果中可得到参数的上限、下限时，可用简化概率分布方法或3σ法(σ为标准差)近似确定参数的均值和标准差。

6.1.6  通过原位测试、室内试验等直接或间接方法确定岩土性能指标和地基、桩基承载力等指标时，应考虑样品扰动、室内外试验条件与实际工程结构条件的差别以及所采用公式误差等因素的影响。

▼ 展开条文说明
6.1.5  岩土性能参数的标准值有可能采用可靠性估值，可根据区间估计理论确定，单侧置信界限值由式求得，式中t_a为学生氏函数，按置信度1—α和样本容量n确定。
当试验数据不足，可用简化概率分布方法或3σ法近似确定岩土参数的数字特征。简化概率分布方法是94版国家标准推荐的方法，该法在岩土工程结构的可靠度分析中有很大实用价值，因为在长期的工程经验和试验基础上，大部分岩土参数都积累了相当多的基础资料。在进行工程设计时，都能从各种设计手册中查到某一参数的上限、下限值。
设基本变量x的上限、下限分别为x_u、x_l，其概率分布根据其变异情况选择概率分布类型，并按表4估算基本变量的平均值和标准差。
表4  常用简化概率分布的平均值和标准差

注：根据保证率的不同，K值取2或3。
3σ法主要利用了正态分布变量99.73％的数据都落在平均值周围3倍标准差范围内的事实。该法需要首先估算参数最大可能的极大值和极小值，若H_CV表示参数最大可能的极大值，L_CV为最大可能的极小值，则参数的标准差：

3σ法以正态分布为基础，但是其他形式的分布也具有类似的性质，因此，该法适用于不同的分布类型。

6.2.1  结构或构件的几何参数a宜采用随机变量概率模型描述，其慨率分布类型应运用参数估计和概率分布的假设检验方法确定。

6.2.2  测试数据不足时，几何参数的统计参数可根据有关标准中规定的公差，经分析判断确定。

▼ 展开条文说明
6.2.1、6.2.2  几何参数是极限状态方程中的一个基本变量，是影响结构抗力的主要因素之一，所以需要研究它的不确定性。一般以调查实测数据为基础，运用参数估计和概率分布假设检验，寻求其统计特征。测试数据不足时，几何参数统计参数可以依据相关标准确定。

6.2.3  几何参数的变异性对结构抗力及其他性能的影响很小时，几何参数的标准值可采用设计规定的名义值。

▼ 展开条文说明
6.2.3  几何参数是结构或构件的几何特征值，包括高度、宽度、面积、面积矩、惯性矩、混凝土保护层厚度、箍筋间距和结构的长度、跨度、偏心矩等，还包括由这些几何参数构成的函数。当结构的某些几何参数，如梁跨，其变异性一般对结构抗力的影响很小，可取设计规定的名义值，而对于如截面几何特性对结构可靠性影响很大的参数，则需要进行统计分析。

7.1.1  结构分析应包括作用效应和抗力以及其他性能分析。作用效应和抗力不能明确区分时，可按照作用的有利和不利情况分别对结构进行分析。

7.1.2  结构分析可采用理论计算、模型试验、原型试验或将上述方法相结合的方法。

▼ 展开条文说明
7.1.1、7.1.2  结构分析是对结构上的作用、作用效应和结构或构件抗力以及它们相互关系了解和认识的过程。当不能明确地将作用效应和抗力区分时，可按照作用有利和不利情况分别对结构进行分析。
结构分析的基本方法有理论计算、模型试验和原型试验等，其中理论计算最为普遍，对某些新型、重要结构或构件，其影响因素复杂，用理论计算难以得到满意结果时，可采用模型试验方法进行分析。当模型试验方法由于尺寸效应不能取得满意结果时，可采用原型试验。在具体分析中，可将这些方法结合使用。

7.1.3  结构理论计算应根据结构类型、材料性能和受力特点等因素，采用线性或非线性分析方法，并应符合下列规定：

   1  结构性能始终处于弹性状态时，应采用弹性理论进行结构分析；

   2  结构在达到极限状态前处于弹塑性状态时，宜采用弹塑性理论进行结构分析；

   3  结构在达到极限状态前能够产生足够的塑性变形，且所承受的不是多次重复的作用时，宜采用塑性理论进行结构分析；

   4  结构的承载力由脆性破坏或稳定控制时，不应采用弹塑性理论分析。

▼ 展开条文说明
7.1.3  结构理论计算要选用合适的分析理论：弹性理论、弹塑性理论、塑性理论，这要根据结构类型、材料性能和受力特点等综合考虑。当结构的材料性能处于弹性状态时，力与变形成线性关系，应采用弹性理论进行结构分析，在这种情况下，分析比较简单，效率也较高；而当结构的材料性能处于弹塑性状态或完全塑性状态时，力与变形之间的相互关系比较复杂，一般情况下都是非线性的，宜采用弹塑性理论或塑性理论进行结构分析。
为保证结构安全，当结构破坏前能够产生足够的塑性变形时，即发生延性破坏时，一般采用塑性理论进行结构分析；当结构的承载力由脆性破坏或稳定控制时，应慎重选择关系模型进行分析。

7.1.4  动力作用对结构产生较大影响时，应对结构进行动力响应分析。

▼ 展开条文说明
7.1.4  结构动力分析主要涉及结构的刚度、惯性力和阻尼。动力分析刚度与静力分析所采用的原则一致。尽管重复作用可能产生刚度的退化，但由于动力影响，也可能引起刚度增大。惯性力是由结构质量、非结构质量和周围流体、空气和土壤等附加质量的加速度引起的。阻尼可以由许多不同因素产生，其中主要因素有：
   (1)材料阻尼，例如源于材料的弹性特性或塑性特性。
   (2)连接中的摩擦阻尼。
   (3)非结构构件引起的阻尼。
   (4)几何阻尼。
   (5)土壤材料阻尼。
   (6)空气动力和流体动力阻尼。
强烈地震时的动力反应，一般需要考虑循环能量衰减和滞回能量消失，并应关注可能的变形限值。

7.1.5  结构分析的精度应能满足结构设计要求，必要时应进行试验验证。

▼ 展开条文说明
7.1.5  铁路工程结构的计算分析分为整体结构分析和局部(构件)分析。整体结构分析时为确定结构不同截面上的纵向力、弯矩、剪力、扭矩等，它是校核局部设计的基础。根据受力特点还要对结构某些特殊部分和各构件进行计算分析。
计算分析需要采用适当的计算模型，计算模型的简化、等效及假定等要反映结构或构件的实际行为状态，并满足设计的精度要求。必要时，还可以借助试验进行辅助设计与验证。

7.1.6  铁路工程结构存在下列情况之一时，可进行试验辅助设计：

   1  缺乏理论模型或足够的数据，不能按现行方法处理；

   2  计算参数或计算结果不能正确反映实际条件；

   3  使用新型结构或构件、新材料或建立新设计公式；

   4  确认设计中的控制性假设。

▼ 展开条文说明
7.1.6  当结构或结构的一部分难以用一般力学计算方法确定其作用效应或抗力时，可用试验辅助设计的方法加以补充。试验辅助设计是利用试验确定结构或构件抗力、材料性能、岩土性能以及结构作用和作用效应设计值的方法，本条列举了需进行试验辅助设计的四种情况。

7.2.1  结构分析采用的基本假定和计算模型，应能合理描述所考虑极限状态下的结构反应。

▼ 展开条文说明
7.2.1  建立结构分析模型一般都要对结构原型进行适当简化，考虑决定性因素，忽略次要因素，并合理考虑构件及其连接，以及构件与基础间的力-变形关系等因素。

7.2.2  根据结构的具体情况，可采用一维、二维或者三维计算模型进行结构分析。

▼ 展开条文说明
7.2.2  一维结构分析模型适用于结构某一维尺寸比其他两维大的多的情况，或结构在其他两维方向上的变化对结构分析结果影响很小的情况，如连续梁；二维结构分析模型适用于结构某一维尺寸比其他两维小得多的情况，或结构在某一维方向上的变化对分析结果影响很小的情况，如框架涵、深梁；三维结构分析模型适用于结构中没有一维尺寸显著大于或小于其他两维的情况。

7.2.3  结构分析模型与实际状况之间的差异，可通过结构极限状态方程中的模型不定性系数加以调整。

▼ 展开条文说明
7.2.3  作用效应及结构构件抗力计算模式的不确定性，是指计算分析结果与实际情况不相吻合的程度。其中包括确定作用效应时采用的计算简图和分析方法的误差，截面抗力计算公式的误差，以及关于作用、材料性能、几何参数统计分析中的误差等。这类误差不是定值而是随机变量，因此在极限状态方程中要引入附加变量——模型不定性系数予以考虑。
模型不定性系数一般通过试验结果与公式计算值之比进行描述，或通过不同精度模型的计算结果相比较，经统计分析并结合工程经验判断确定，模型不定性常反映在分项系数中。在有条件的情况下，可以通过校准法分析确定。

7.2.4  在不能利用统计分析确定作用参数时，应给出作用参数的上下限范围，并通过比较确定对结构不利作用的取值。

7.2.5  动力作用可被认为是拟静力作用时，可通过把动力作用分析结果包括在静力作用中或对静力作用乘以等效动力放大系数等方法，来考虑动力作用效应。

▼ 展开条文说明
7.2.5  当允许结构进行简化分析时，可计算“准静态作用”响应，并乘以动力系数作为动态作用的响应。

7.2.6  动力作用引起的动力响应使结构有可能超过正常使用极限状态的限值时，应根据实际情况构建模型对结构进行正常使用极限状态验算。

▼ 展开条文说明
7.2.6  振动响应与动力作用息息相关，若动力作用引起的动力响应如振幅、加速度、列车运行安全性和旅客舒适性等指标有可能超限或根据设计经验无法直接判断时，需根据实际情况构建模型对结构进行正常使用极限状态验算。

7.2.7  铁路工程结构构建疲劳作用模型时，应按照下列特征之一确定其参数：

   1  完整的应力幅历程；

   2  应力幅以及相应的循环次数。

▼ 展开条文说明
7.2.7  疲劳破坏一般起源于初始缺陷或应力集中处，在多次重复荷载作用后，可能出现裂纹或断裂，进而不适用于继续承载而发生疲劳破坏。在描述疲劳作用模型时，需要了解应力幅历程或应力谱，前者对应完整的应力幅历程，后者对应应力幅及其循环次数。

7.3.1  试验辅助设计可根据需要进行下列试验：

   1  确定作用或作用效应的试验；

   2  用规定的实验方法获得材料、岩土性能的试验；

   3  在给定荷载条件下，直接确定结构或构件极限承载力或使用性能的试验；

   4  结构或模型整体试验。

▼ 展开条文说明
7.3.1  试验辅助设计以试验数据的统计评估为依据，与概率设计和分项系数设计概念相一致。采用试验辅助设计的结构，要达到相关设计状况采用的可靠性水平，此时材料性能、模型参数或抗力设计值的确定要符合下列基本原则：
(1)采用经典统计方法或贝叶斯(Bayesian)法推断材料性能、模型参数或抗力的设计值：先确定标准值，然后除以一个分项系数，必要时考虑换算系数的影响；换算系数应通过试验并结合理论分析确定，理论分析应包括尺寸效应、时间效应、边界条件、影响材料性能的环境条件、工艺条件等影响因素。
(2)在进行材料性能、模型参数或抗力设计值评估时，要考虑试睑数据的离散性、与试验数量相关的统计不定性和先验的统计知识。
试验结果统计分析时要考虑统计不定性的影响，具体统计方法有两种：
经典统计法。
(1)当性能X服从正态分布时，其设计值Xd与标准值Xk关系如下：

式中：ηd——转换系数；
     γm——材料性能分项系数，根据材料通常采用的值和所考虑的失效模型来规定。当试验状况与标准设计状况相差过大，以致不能选定具有足够置信度的分项系数时，则优先采用Bayesian方法：
     μx、δx——抗力样本平均值和变异系数；
     kn——样本容量系数，取决于试件数目和选定的置信度。表5给出了分位值为0.05，置信度为0.75时的kn值。

(2)当性能X服从对数正态分布时，其标准值为：

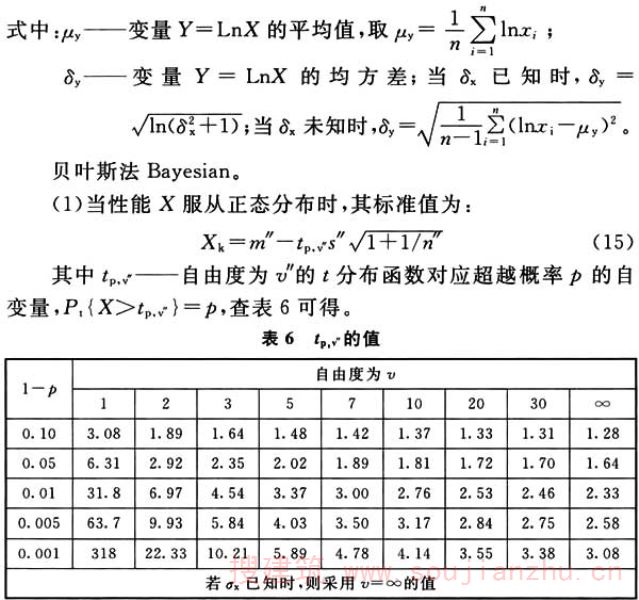
先验分布有四个参数m′、n′、s′、v′。将特征化的先验资料与具有样本平均值m和样本标准差s的n次观测试验结果组合起来，得到X的未知平均值和标准差的后验分布。此时参数规定如下：

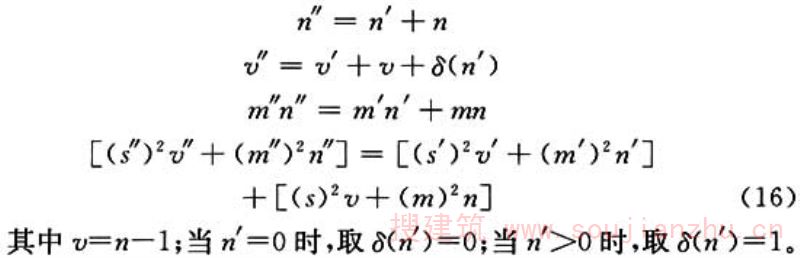
(2)先验分布参数n′和v′的确定，要符合下列原则：
       1)当有效数据很少，则取n′和v′为0。在这种情况下，最后结果将与Bayesian法相同。
       2)根据过去的经验，平均值和标准差几乎可以取定值，则n′和v′可以给予相对较高的值，如取50或更大。
       3)在一般情况下，假定只有很少数据或无先验数据，此时n′＝0，这样就有可能获得较佳的估计值。

7.3.2  试验前应制定一个符合相关技术标准的试验方案，选择的试验环境和加载顺序应能正确预测实际结构的性能。原型试验宜做到与实际结构的几何尺寸、作用和环境条件等相符；模型试验中模型的相似性和边界条件等应能反映结构设计的极限状况。

7.3.3  以试验结果为基础进行设计时，应考虑实际构件质量控制、尺寸效应、时间效应、边界条件、工艺条件、环境条件等与试验的差异。

7.3.4  采用试验辅助设计的结构，应达到相关设计状况采用的可靠性水平。

▼ 展开条文说明
7.3.2～7.3.4  试验辅助设计需要符合下列要求：
   (1)在试验进行之前，制定试验方案。试验方案包括试验目的、试件的选取和制作，以及试验实施和评估等所有必要的说明。
   (2)为制定试验方案，要预先进行定性分析，确定所设计结构或构件性能的可能临界区域和相应极限状态标志。
   (3)加工合适尺寸和与实际生产相同工艺的试件，使试验能够再现所设计构件的实际应用性能，根据试验要求和为试验选定的相关状况进行组装。
   (4)试验除记录该极限状态的机制、边界条件和最终值外，还要观察试验过程中与超出预先考虑的极限状态有关的各种现象。
   (5)试验需由具有相应资质的技术人员和(或)机构完成。
   (6)除统计评估试验结果外，有关结构性能的一般理论和普遍接受的设计规则在进行试验设计时仍然有效。
   (7)专门试验得出的结论与试验范围内结构的性能和生产工艺有关。除非理论分析证明所得结论可以推广到其他构件类别，否则扩大结论应用范围需有新的试验。
尽管要求试验与设计中的实际情况尽可能相符合，但仍会不可避免地出现各种差异，包括尺寸效应、时间效应、边界条件、湿度条件、工艺条件等，当将试验结果用于设计时，应考虑这些差异，否则会使设计的结构或同类结构的可靠度不同。试验条件与实际条件的差异可以通过换算系数处理，具体由理论分析和试验结果判断确定。
当设计以模型试验或原型试验为基础时，原型试验宜做到与实际结构的几何尺寸、作用和环境条件等相符。模型试验包括缩尺模型和相似模型，一般应满足几何相似、力学相似和材料相似，以保证模型试验的结果能够推演到原型结构的工作性能，并考虑试验模型与实际构件的差异，试验误差和试验结果的统计不定性(小子样统计方法)，即按试验结果确定设计值时，需考虑试验数量的影响。

8.1.1  分项系数可分为作用分项系数和抗力分项系数。

▼ 展开条文说明
8.1.1  铁路工程结构极限状态设计是采用基本变量及其分项系数表达的设计式，通过分项系数考虑各个基本变量的变异性和不定性对结构可靠性水平的影响。
分项系数分为作用分项系数和抗力分项系数。作用分项系数是指在设计计算中，反映作用不定性并与结构可靠度相关联的分项系数，如永久作用分项系数、可变作用分项系数；抗力分项系数是反映抗力不定性并与结构可靠度相关联的分项系数；材料性能分项系数是反映材料性能不定性并和结构可靠度相关联的分项系数，有时用以代替抗力分项系数。

8.1.2  分项系数宜根据有关基本变量的概率分布和统计参数及规定的可靠指标，通过计算分析，并结合工程经验，经优化确定。缺乏统计数据时，可根据传统的或经验的设计方法，采用有关标准规定的分项系数。

▼ 展开条文说明
8.1.2  分项系数是根据可靠度分析并与规定的目标可靠指标相对应来确定的，在保证相同目标可靠指标情况下，分项系数的确定会有多种方案。优化确认的一组分项系数应使设计的铁路工程计算得到的可靠指标逼近目标可靠指标。
确定分项系数宜遵循两点：同一种作用，在不同铁路工程结构中宜采用相同的分项系数；同一种材料，在不同铁路工程结构中宜采用相同的分项系数。
慨率极限状态设计方法必须以统计数据为基础，考虑到各类工程结构所具有的统计数据在质和量两个方面都有很大差异，某些领域甚至没有统计数据，因而规定当缺乏统计数据时，可以不通过可靠指标直接按工程经验确定分项系数。

8.1.3  铁路工程桥涵结构列车荷载作用分项系数宜取1.4～1.5。

▼ 展开条文说明
8.1.3  20世纪90年代，我国铁路桥涵结构可靠性设计规改时，对列车活载分项系数进行了大量计算，推荐列车活载分项系数取1.4，成果反映在中国铁设(原铁三院)主编的2011版《铁路桥涵设计规范(极限状态设计法)》中，其量值为1.4；中铁咨询通过试设计表明，列车活载分项系数采用1.45的设计计算结果与现行桥规更接近；考虑到目前铁路桥涵结构恒活载比值远远大于原有设计情况，活载分项系数可以适当增大。根据《铁路工程结构荷载分项系数确定研究》(专项编制2012-01)的研究成果，铁路桥涵结构列车活载竖向作用一般情况下取1.4～1.5较为合适，铁路隧道、路基和轨道结构荷载分项系数的制定可根据课题研究提供的方法另行确定。

8.2.1  铁路工程结构作用F的设计值Fd可由下式确定：

   式中：Fr——作用的代表值；

         γF——作用的分项系数。

▼ 展开条文说明
8.2.1  设计值一般表示为作用代表值与作用分项系数的乘积。组合值、频遇值和准永久值通过对可变作用标准值的折减来表示，即分别对可变作用的标准值乘以不大于1的组合值系数、频遇值系数和准永久值系数。本条作用分项系数为γ_F，不仅包含作用值向不利方向偏离代表值的可能性，还考虑了作用模型不定性影响。

8.2.2  材料或产品性能的设计值fd可由下式确定：

   式中：fk——材料或产品性能的标准值；

         γM——材料或产品性能的分项系数，考虑模型不定性和(或)几何参数偏差等影响；

         γRd——抗力模型不定性系数，一般取1.0；

         γm——材料或产品性能的分项系数。

▼ 展开条文说明
8.2.2  材料或产品性能的分项系数，要考虑相对于材料或产品性能特征值不利偏差的可能性、样本容量和缩尺效应影响、湿度和温度影响、其他相关参数影响等。此外建议将抗力计算模型不定性和(或)几何参数的其他偏差效应等影响统一在材料或产品性能分项系数中予以考虑，故本条分项系数为γ_M。如果不含模型不定性影响，材料或产品性能分项系数为γ_m。

8.2.3  几何参数的设计值确定应符合下列规定：

   1  几何参数的设计值可采用名义值表达：

   式中：ad——几何参数的设计值；

         anom——几何参数的标准值或名义值。

   2  几何参数的变异性对构件可靠度有重要影响时，几何参数的设计值可通过下式确定：

   式中：ad——几何参数的设计值，代表几何缺陷时，anom＝0，△a≠0；

         △a——几何参数的附加量。考虑使用名义值(或标准值)不利偏差的可能性，或考虑数个偏差同时发生的累积效果。

8.2.4  结构抗力的设计值Rd按材料性能确定时，结构抗力的设计值应按式(8.2.4-1)确定。结构抗力的设计值按岩土性能或静力平衡确定时，结构抗力的设计值也可按式(8.2.4-2)确定：

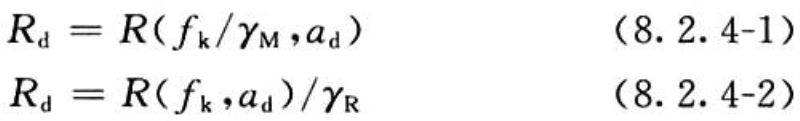
   式中：R(·)——抗力R的代表函数，括号内为该函数式的参变量。

8.3.1  铁路工程结构或构件按承载能力极限状态设计应符合下列规定：

   1  结构或构件(包括基础等)破坏或过度变形的承载能力极限状态设计，应满足下式要求：

   式中：Sd——结构作用效应设计值；

         Rd——结构抗力设计值。

   2  整个结构或其一部分作为刚体失去静力平衡的承载能力极限状态设计，应满足下式要求：

   式中：Sd,dst——不平衡作用效应的设计值；

         Sd,stb——平衡作用效应的设计值。

▼ 展开条文说明
8.3.1  本条列出了两类情形下承载能力极限状态的设计表达式。

8.3.2  铁路工程结构重要性系数γ0，应按表8.3.2采用。

表8.3.2   铁路工程结构重要性系数γ0

▼ 展开条文说明
8.3.2  铁路工程结构重要性系数与结构的安全等级协调一致。安全等级为二级的铁路工程结构，其重要性系数取为1.0。安全等级为一级和三级的铁路工程结构，重要性系数分别取1.1和0.9。考虑到不同投资主体对结构可靠性要求可能不同，故允许安全等级为一级的结构重要性系数不小于1.1。

8.3.3  铁路工程结构按承载能力极限状态设计的作用组合可采用基本组合、偶然组合和地震组合。

▼ 展开条文说明
8.3.3  结构的承载能力极限状态设计，按照可能出现的作用，将其分为三种作用效应组合，即基本组合、偶然组合和地震组合。作用效应的基本组合是指永久作用设计值效应与可变作用设计值效应的组合，这种组合用于结构的常规设计，是所有结构都需考虑的。作用效应的偶然组合是指永久作用标准值、可变作用代表值和一种偶然作用设计值的组合。作用效应的地震组合是指永久作用标准值、可变作用代表值和地震作用设计值效应的组合。

8.3.4  持久设计状况和短暂设计状况可采用作用的基本组合，作用效应设计值的计算应符合下列规定：

   1  作用效应设计值按下式确定：

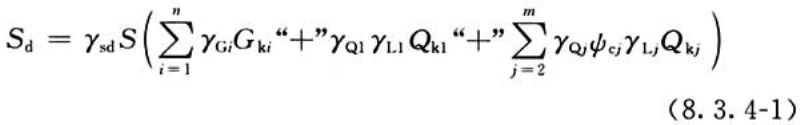
   式中：γsd——计算模型不定性系数，可取1.0；

         γGi——第i个永久作用的分项系数；

         Gki——第i个永久作用的标准值；

         γQ1——主导可变作用的分项系数；

         Qk1——主导可变作用的标准值；

         γQj——第j个其他可变作用的分项系数；

         γL1、γLj——第1个和第j个考虑结构设计使用年限的荷载调整系数，应按有关规定采用，对设计使用年限与设计基准期相同的结构，可取1.0；

         ψcj——第j个可变作用的组合值系数；

         Qkj——第j个其他可变作用(荷载)的标准值。

   2  作用效应与作用可用线性关系表达时，作用效应设计值可按下式确定：

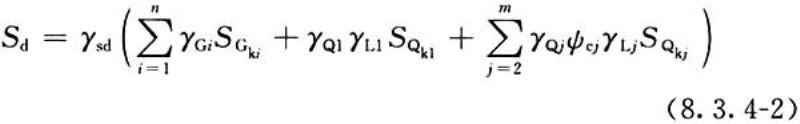
   式中：SGki——第i个永久作用标准值效应；

         SQk1——主导可变作用标准值效应；

         SQkj——第j个其他可变作用标准值效应。

▼ 展开条文说明
8.3.4  为了使设计式所隐含的可靠指标(即计算可靠指标)与设计目标可靠指标一致，在实用设计式中引入一个作用效应计算模型不定性系数(一般取1.0)，以便对设计式所隐含的可靠指标进行调整。计算式中“＋”表示与之组合。

8.3.5  偶然设计状况应采用作用的偶然组合，作用效应设计值的计算应符合下列规定：

   1  作用效应设计值可按下式确定：

   式中：Ad——偶然作用的设计值；

         ψf1——主导可变作用的频遇值系数；

         ψq1、ψqj——主导可变作用和其他可变作用的准永久值系数。

   2  作用效应与作用可用线性关系表达时，作用效应设计值可按下式确定：

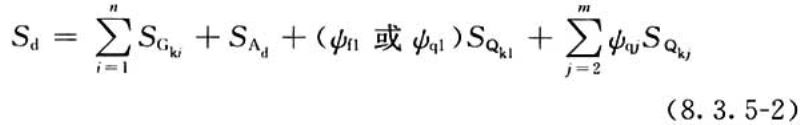
▼ 展开条文说明
8.3.5  偶然作用有唯一的特征值，该值也用作设计值。

8.3.6  地震设计状况应采用作用的地震组合，作用效应设计值的计算应符合下列规定：

   1  地震组合的作用效应设计值宜根据重现期为475年的地震作用确定，其效应设计值应符合下列规定：

       1)作用效应设计值宜按下式确定：

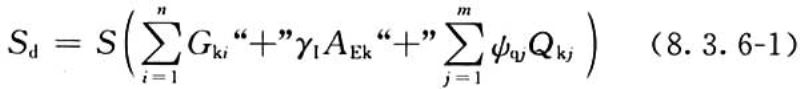
   式中：γⅠ——地震作用重要性系数，应符合现行国家标准《铁路工程抗震设计规范》GB 50111的规定；

         AEk——根据重现期为475年的地震作用(基本烈度)确定的地震作用的标准值。

       2)作用与作用效应可用线性关系表达时，作用效应设计值可按下式计算：

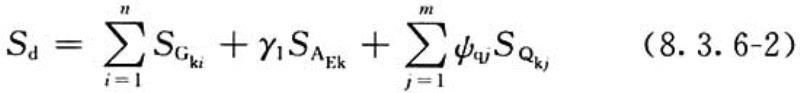
   2  地震组合的作用效应设计值，也可根据重现期大于或小于475年的地震作用确定，并应符合有关抗震设计标准的规定。

   3  当采用减隔震设计时，应考虑减隔震装置对作用效应的影响。

▼ 展开条文说明
8.3.6  铁路工程结构地震设计组合应符合现行国家标准《铁路工程抗震设计规范》GB 50111中的相关规定。针对目前广泛采用的减隔震设计，应考虑减隔震装置对作用效应的折减。

8.3.7  设计中应采用不同的分项系数来考虑永久作用的有利和不利影响。当永久作用对结构或构件的承载力起有利情况时，永久作用分项系数γG的取值不应大于1.0。

▼ 展开条文说明
8.3.7  设计一般不考虑作用的有利影响。当永久作用效应对结构或构件承载力产生有利影响时，要求永久作用分项系数γ_G的取值不大于1.0。

8.4.1  铁路工程结构按正常使用极限状态设计可按下式确定：

▼ 展开条文说明
8.4.1  正常使用极限状态涉及构件的适用性，设计表达式中的限值，按照可以接受的变形、加速度、裂缝宽度、振动等考虑随机性后以统计方式或经验方式确定。

8.4.2  铁路工程结构按正常使用极限状态设计的作用组合可采用标准组合、频遇组合和准永久组合。

▼ 展开条文说明
8.4.2  结构的正常使用极限状态设计，按照可能出现的作用，需考虑可变作用的标准组合、频遇组合和准永久组合，其可变作用代表值采用标准值、频遇值和准永久值。设计时，根据结构作用的情况，采用相应的组合。

8.4.3  标准组合的作用效应设计值的计算应符合下列规定：

▼ 展开条文说明
8.4.3  正常使用极限状态设计中作用和抗力的分项系数取为1.0，故在设计表达式中不出现分项系数项。

8.4.4  频遇组合的作用效应设计值的计算应符合下列规定：

8.4.5  准永久组合的作用效应设计值的计算应符合下列规定：

8.5.1  承受重复荷载作用的铁路工程结构应根据其设计使用年限选定适当的疲劳目标可靠指标，疲劳目标可靠指标可按本标准第4.3.9条规定的方法选定。

8.5.2  直接承受列车重复荷载作用的结构或构件，应根据设计基准期内变幅重复荷载或荷载效应的统计特征，制定相应的疲劳荷载谱和标准荷载效应比频谱，作为疲劳作用分项系数制定的依据。铁路列车疲劳荷载谱和标准荷载效应比频谱，可按本标准附录B.4规定的方法确定。

▼ 展开条文说明
8.5.1、8.5.2  铁路工程结构承受较大列车动荷载的反复作用，该作用产生的应力虽低于结构的名义承载能力，但由于结构中有微小的缺陷或焊接残余应力及应力集中，易萌生裂纹。随着外力循环次数的增加，微小裂纹会逐渐扩展，最后导致断裂，即产生疲劳破坏，为防止疲劳断裂，需进行疲劳极限状态的设计和检算。
根据科研项目《铁路桥梁结构疲劳极限状态设计方法研究》(2012G014-C)的研究成果，铁路桥梁结构疲劳设计目标可靠指标为3.5，据此研究得出了疲劳设计分项系数，提出了铁路桥梁在更新参数后的疲劳设计方法，这为第三层次规范的编制提供了基础。

8.5.3  铁路工程钢结构或钢构件应按下列方法之一进行疲劳极限状态验算：

   1  采用等效等幅重复应力法进行疲劳极限状态验算，应满足下式要求：

   式中：γsd——计算模型不定性系数；

         γfat——钢结构疲劳作用分项系数，可取1.0；

         △σe——钢结构验算部位等效等幅重复应力幅标准值(计入运营动力系数、离心力)；

         △σ0——疲劳设计强度，；

         γaf——钢结构验算部位材料(或构造细节)的疲劳抗力分项系数；

         △faek——钢结构验算部位材料(或构造细节)的等幅疲劳强度标准值。

   2  采用极限损伤度法进行疲劳极限状态验算，应满足下式要求：

   式中：ni——应力谱为△σi的循环次数；

         Ni——按应力幅△σi所推导的致伤循环次数。

▼ 展开条文说明
8.5.3  钢结构疲劳可靠性验算一般有两种方法：等效等幅重复应力法和极限损伤度法。
等效等幅重复应力法中，首先求得结构危险部位材料(或构造细节)的应力谱，并用适当的换算方法，如Miner准则，求得对应于这一应力谱的等效重复应力。这样使得原来需要用随机过程来表达的应力历程简单地用随机变量来表述，结构的变幅重复应力采用等效重复应力表达后，其疲劳设计式可用作用效应和抗力设计式表达。这里作用效应是结构危险部位材料(或构造细节)的等效重复应力，抗力就是相应材料(或构造细节)的等幅疲劳强度。
极限损伤度法是将结构危险部位材料(或构造细节)的变幅重复应力分为若干级，然后根据Miner准则求得相应部位的损伤度，求算累积损伤度D不大于1的验算方法。
进行疲劳极限状态可靠性检算时，由于等效等幅重复应力法比较简便和偏于安全，首先采用该法，检算不通过时再用极限损伤度法，用极限损伤度法检算再不符合要求者，则要重新设计。
△faek是根据钢结构验算部位(或构造细节)的S-N曲线，取循环次数为ne的等幅疲劳强度(以应力幅计)作为验算部位(或构造细节)的等幅疲劳强度标准值。钢结构等效等幅重复应力的循环次数ne可以选为1×107次，必要时也可以选用其他能反映变幅重复应力循环特征的次数。

8.5.4  铁路工程混凝土结构应按下列方法之一进行疲劳极限状态验算：

   1  采用等效等幅重复应力法进行疲劳极限状态验算，应满足下式要求：

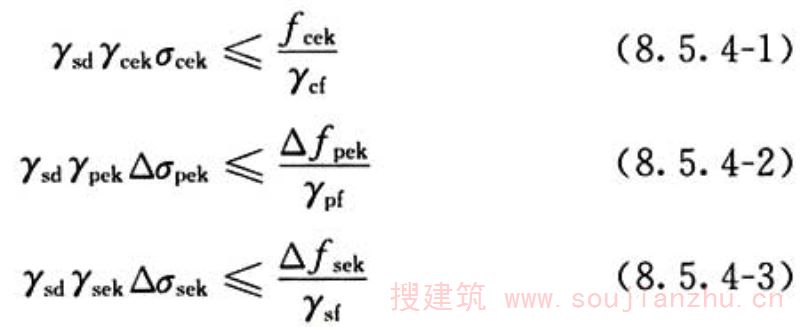
   式中：γcek、γpek、γsek——分别为混凝土、预应力钢筋、钢筋的疲劳作用分项系数；

         σcek、△σpek、△σsek——分别为混凝土结构验算部位的混凝土等效疲劳应力标准值、预应力钢筋等效疲劳应力幅标准值、钢筋等效疲劳应力幅标准值(计入运营动力系数、离心力)；

         fcek、△fpek、△fsek——分别为混凝土结构验算部位的混凝土、预应力钢筋、钢筋的等幅疲劳强度标准值；

         γcf、γpf、γsf——分别为混凝土、预应力钢筋、钢筋的疲劳抗力分项系数。

   2  采用极限损伤度法进行疲劳极限状态验算，应符合本标准第8.5.3条第2款的规定，其中验算对象分别为验算部位的混凝土、预应力钢筋和钢筋。

▼ 展开条文说明
8.5.4  混凝土结构疲劳可靠性的验算方法同样包括等效等幅重复应力法和极限损伤度法。当按等效等幅重复应力法进行混凝土结构疲劳极限状态可靠性验算时，等效等幅重复应力循环次数ne一般为2×106次。

9.1.1  铁路工程结构的勘察设计、施工、使用和维护的可靠性管理，应符合本标准附录C的规定和有关标准的专门规定。

9.1.2  铁路工程结构设计应符合国家现行抗震、耐久性等标准的有关规定。

9.1.3  铁路工程结构设计应对结构可能受到的偶然作用、环境影响等采取必要的防护措施。

9.1.4  铁路工程结构的材料及施工过程应进行质量控制，按铁路现行有关标准的规定进行竣工验收。

9.1.5  铁路工程结构应按设计规定的运营条件使用，并进行必要的维护和维修。

▼ 展开条文说明
9.1.1～9.1.5  铁路工程结构达到规定的可靠性水平是有条件的，结构可靠度是在“正常设计、正常施工、正常使用”条件下结构完成预定功能的概率，本节是从实际出发，对“三个正常”要求做出的规定。

9.2.1  既有铁路工程结构出现下列情况之一时，应进行可靠性评定：

   1  结构的使用时间超过规定的年限；

   2  结构的用途或使用要求发生改变；

   3  结构的使用环境出现恶化；

   4  结构存在较严重的质量缺陷；

   5  出现影响结构安全性、适用性或耐久性的材料性能劣化、构件损伤或其他不利状态；

   6  对既有结构的可靠性有怀疑或有异议。

9.2.2  既有铁路工程结构可靠性评定的评定内容、评定步骤和方法等，应符合本标准附录D的规定。

▼ 展开条文说明
9.2.1、9.2.2  本节提出对既有铁路工程结构可靠性评定的建议。第9.2.1条第1款中的“规定的年限”不仅限于设计使用年限，铁路行业规定大修周期，当使用5年～10年就要进行检测鉴定，重新备案。出现第4款和第6款的情况，当争议的焦点是设计质量和施工质量问题时，可以先进行工程质量的评定，再进行可靠性评定。
把安全性、适用性、耐久性和抗灾害能力等评定内容分开可以避免概念的混淆，避免引发不必要的问题，同时便于运维管理部门根据问题的轻重缓急采取适当的处理措施。对既有铁路工程结构进行可靠性评定时，可以根据结构的具体情况提出进行某项性能的评定，也可以进行全部性能的评定。

A.1.1  采用分位值法计算结构可靠指标应符合下列规定：

   结构或构件的可靠指标计算宜借助计算机编程实现(图A.1.1)。

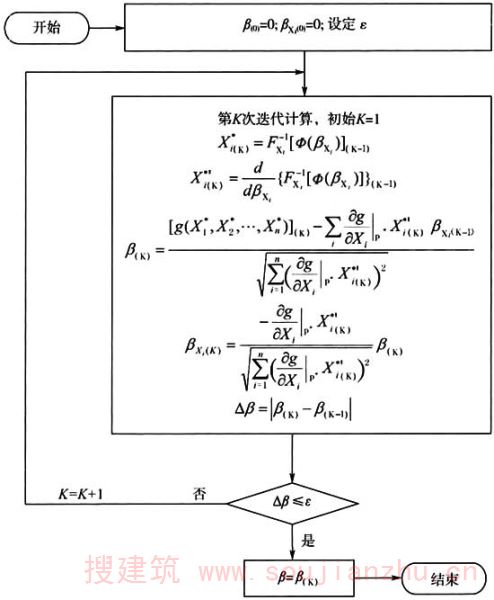
图A.1.1  分位值法计算可靠指标框图

   3  服从正态分布、对数正态分布、极值Ⅰ型分布和三参数对数正态分布的随机变量X的分位值X*i和分位导数X*′i可按表A.1.1计算。

表A.1.1  随机变量X的分位值和分位导数计算公式

▼ 展开条文说明
A.1.1  结构可靠性分析是以基本变量为前提条件。基本变量可以用概率分布模型和统计参数(均值、标准差、变异系数等)描述。概率分布模型由适量的试验、调研数据经概率统计方法确定，或由经验确定。
基本变量可以与相关变量及模型不定性变量构成综合基本变量，并用相应的概率模型和统计参数描述。
按本附录进行可靠性分析和设计时，需要具备下列条件：
   (1)具有结构极限状态方程；
   (2)基本变量具有正确、可靠的统计数据及概率分布。
铁路工程结构可靠度计算分析中常用的三种概率分布模型及统计参数如下：


一般永久作用(荷载)或可变作用(荷载)的任意时点分布可以用正态分布模型化；材料性能及几何尺寸可以用对数正态分布或正态分布模型化；风载等可以用极值Ⅰ型分布模型化。
结构可靠度的计算方法有多种：如近似分析法，蒙特卡罗法，数值积分法等，近似分析法又包括一阶可靠度方法、二阶可靠度方法等。
分位值法属于一阶可靠度方法，其计算可靠度的基本原理就是把服从任意分布的随机变量转换为标准正态分布变量，称为约化高斯变量，服从标准正态分布后的计算理论比较成熟，即可求解。
以下是分位值法计算可靠指标的简单说明。

   式中：F(X_i)——基本变量Xi的分布函数；
         Φ(*)——标准正态分布函数；
         βX_i——基本变量Xi的约化高斯变量，又称基本变量的分项可靠指标，为标准正态变量。
用约化高斯变量βX_i为坐标的多维空间来表示的极限方程式为一超曲面，见图2。

A.1.2  结构极限状态方程由独立的任意分布随机变量构成时，可采用JC法按下列步骤计算结构可靠指标：

   1  非正态分布随机变量X，其均值为μX，标准差为σX，可按下列原则将其转换为等效正态分布随机变量：

   式中：μX′、σX′——等效正态分布随机变量X′的平均值和标准差；

         fX′(·)、FX′(·)——等效正态分布随机变量X′的概率密度函数和概率分布函数；

         φ(·)、Φ(·)、Φ-1(·)——标准正态分布的概率密度函数、分布函数和分布函数的反函数。

   2  等效正态分布随机变量X′的平均值和标准差确定后，可采用其他方法计算结构的可靠指标。

▼ 展开条文说明
A.1.2  本条是关于一阶可靠度方法中的JC法，JC法是通过当量正态化以考虑任意分布随机变量。当量正态化的等效原则是在验算点处，非正态随机变量与正态随机变量的慨率分布函数和概率密度函数相等。
非正态随机变量可靠指标计算，由分位值法和JC法求得的结果基本一致。

A.1.3  结构极限状态方程可采用蒙特卡罗(Monte-carlo)法按下列步骤计算可靠指标：

   1  选取一组具有代表性的结构或构件，其结构功能函数为Z＝g(X1，X2，…，Xn)＝0，X1，X2，…，Xn为随机变量；

   2  通过随机抽样产生已知分布变量的随机数，x1，x2，…xn；

   3  计算功能函数值Zi＝g(x1，x2，…，xn)；

   4  设抽样次数为N，每组随机变量计算得到的功能函数值为Zi，Zi≤0的次数为L，则在大批抽样之后，结构的失效概率Pf＝L／N；

   5  由失效概率反求可靠指标。

▼ 展开条文说明
A.1.3  本条是蒙特卡罗(Monte-Carlo)法求算可靠指标的步骤，该方法在岩土工程可靠性计算中应用普遍。

A.2.1  结构按校准法确定目标可靠指标应按下列步骤计算：

   1  选取一组具有代表性的结构或控制结构安全的构件作为校准法的计算对象。

   2  在这一组结构或构件中，根据工程用量和重要性，确定各结构的权系数wi。各结构权系数的总和应符合下式规定：

   式中：wi——第i种结构的权系数。

   3  确定各结构或构件的作用效应和抗力中各基本变量的概率分布类型和设计参数。分析传统设计方法的表达式，如受弯表达式、受剪表达式等。

   4  分别计算各结构或构件的可靠指标βi。

   5  计算各结构或构件的加权平均可靠度值βave：

   6  根据加权平均可靠度值βave，经过综合分析，确定结构的目标可靠指标βnom。

▼ 展开条文说明
A.2.1  限于目前统计资料不够完备，一般采用“校准法”为基础确定目标可靠指标。所谓“校准法”，就是通过对原有规范可靠度的反演计算，找出隐含于原有规范下结构的安全指标值，经过综合分析调整，据以制定今后设计采用的目标可靠指标，这实质上是对长期实践证明了的标准规范的现实继承。该法在总体上承认了以往规范的设计经验和可靠性水平，同时也考虑了源于客观实际的调查统计分析资料，是比较现实和稳妥的。
校准对象一般根据权重不同选择代表性的结构或构件，如通用图设计的结构和(或)安全裕度处于临界状态的结构或构件。
本条提供了结构可靠度校准的常规步骤。对于不同工程结构，可靠度校准可以根据具体情况给予适当调整。
随着国家经济发展，在条件具备时可以对结构或构件的可靠度进行调整，但也要以校准后的结果为依据。

A.2.2  目标可靠指标的选择宜考虑结构或构件的失效后果和性质，涉及经济损失、社会和环境影响、自然资源的可持续利用以及降低失效概率所要增加的成本。目标可靠指标也可采用风险水平类比法或费用效益分析法确定。

▼ 展开条文说明
A.2.2  除了校准法，目标可靠指标也可采用风险水平类比法或费用效益分析法确定。
   (1)风险水平类比法。
通过研究其他人类活动的风险水平，确定一个为公众所能接受的失效概率或可靠指标。表7显示了一些事故的一般风险及典型年平均失效率。
表7  不同事故造成的年死亡率

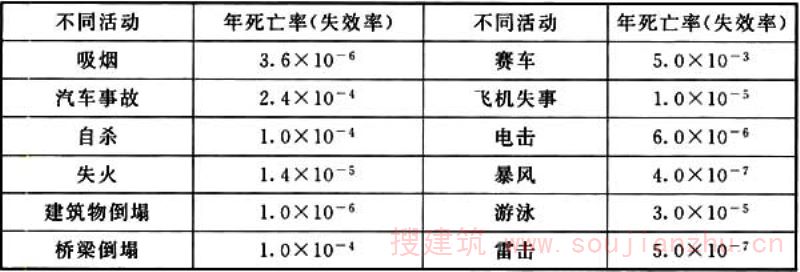
据调查研究，当事故的危险率达到每人每年10^-5时，人们便感到比较安全，但仍要考虑。当事故的危险率降到每人每年10^-6时，人们就不太考虑了。
采用该方法确定目标可靠指标有其困难之处，原因在于对风险水平的接受程度因人而异，没有一个统一的方法来比较不同原因造成的风险，而且该方法不能区分出名义和实际失效概率。
   (2)费用效益分析法。
该法目的是处理费用与期望效益的关系：降低失效概率可以得到更好的效益但会增加制造、安装和维修等费用。费用包括以下几项：投资成本和需要更换的项目费用、安装费用、运营费用和维修费用等。为使投资有意义，应取期望效益值与费用成本差值Z(p)的最大值：

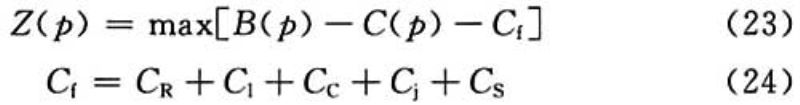
式中：B(p)——期望效益值；
         C(p)——建造成本；
         C_f——失效成本；
         C_R——修理和维护成本；
         C_l——重建成本；
         C_C——功能失效成本；
         C_j——治疗受伤人员成本；
         C_S——拯救人员生命成本。
根据生活质量指数LQI建立生命价值转换函数，可以得到拯救生命的最优费用值，即降低单位死亡人数的潜在货币价值ICAF：

式中：g——人均年国内生产总值；
         e——预期寿命；
         w——预期寿命中用于工作的比例。
ICAF越低，表明风险减小措施越符合低成本高效益的原则，即所花费的单位货币可以挽救更多人的生命。
则拯救生命数为Nf的总费用为C_S＝(ICAF)N_f。

A.3.1  结构或构件设计表达式中分项系数应按下列原则确定：

   1  结构上的同种作用宜采用相同的作用分项系数，不同的作用应采用各自的作用分项系数；

   2  不同种类的构件宜有各自的抗力分项系数，同一种构件在任何可变作用下，抗力分项系数宜不变；

   3  各种构件在不同的作用效应比下，按所选定的作用分项系数和抗力分项系数进行设计，应使计算可靠指标与目标可靠指标βnom具有最佳的一致性。

▼ 展开条文说明
A.3.1  本条规定了确定结构或构件设计表达式中分项系数的原则。确定设计分项系数的目的，是为了将铁路工程结构的目标可靠指标落实到基于概率理论的极限状态设计表达式中，以使概率极限状态设计的复杂数值运算转化为简单的代数运算。因此，分项系数与目标可靠指标是相互匹配的。

A.3.2  承载能力极限状态设计式中基本变量分项系数的选定应符合下列规定：

   1  极限状态设计式中各基本变量理论分项系数应按下列步骤选定：

       1)结构的极限状态设计表达式可按下式表达。

       2)式(A.3.2-1)中仅有一个可变作用(或组合可变作用)时，可按分位值法或其他适当的方法确定各基本变量的理论设计值。

       3)在目标可靠指标βnom确定情况下，按分位值法确定理论设计值Xid时，可采用迭代法(图A.3.2)按下列公式计算确定。

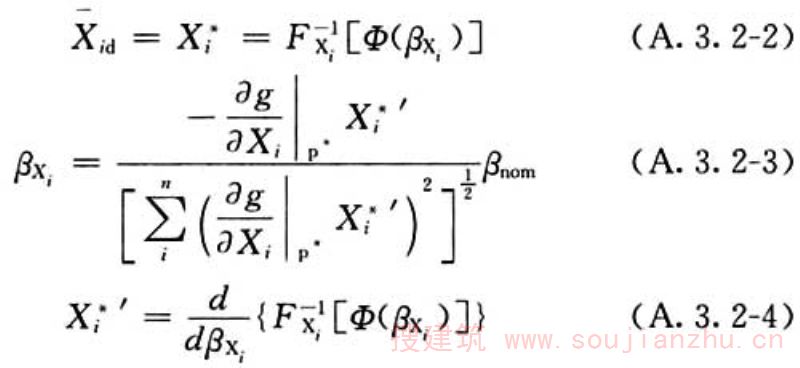
       4)各基本变量的理论设计值Xid与相应标准值之比求算理论分项系数γXi，其中理论作用分项系数为作用理论设计值与作用标准值之比，理论抗力分项系数为抗力标准值与抗力理论设计值之比。

   2  设计分项系数可按下列步骤选定：

       1)结构设计计算工况的选定，可选择极限状态设计式可行域内具有代表性的若干种设计计算工况，确定各自常用的作用效应比；

       2)理论分项系数的计算，可采用第A.3.2条第1款规定的分位值法或其他适当的方法，求得给定目标可靠指标和各种设计计算工况下各基本变量Xi的理论分项系数γXi；

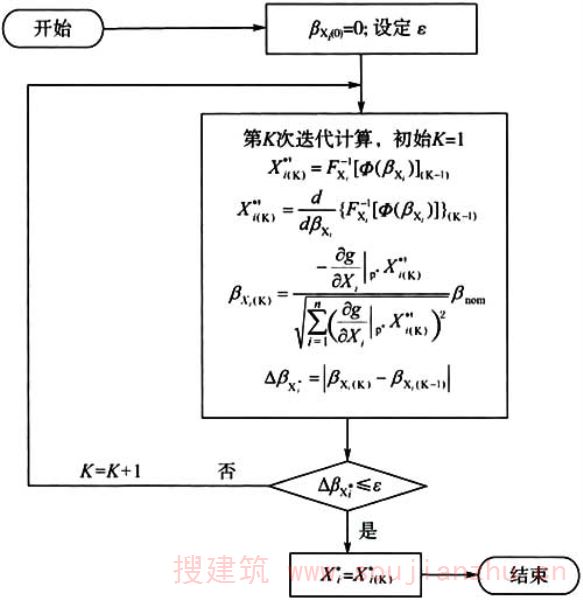
图A.3.2  分位值法确定理论设计值的计算框图

       3)设计分项系数的选定，根据各基本变量的理论分项系数，采用加权平均的方法，选定设计分项系数的初值，试算各种设计计算工况下的结构可靠指标。调整各分项系数以实现计算可靠指标与目标可靠指标的最佳的一致性，据此确定最终的设计分项系数。

   3  铁路工程结构中，涉及材料性能的抗力分项系数，也可根据工程经验或有关标准等综合分析确定。

▼ 展开条文说明
A.3.2  计算分项系数的过程大体与采用分位值法计算β值相同，只是β已知，需采用迭代法求出分项可靠指标βXi，进而求出理论设计值X*i。
当极限状态方程为R—σSG—σSQ＝0时，各随机变量理论分项系数γxi可按下式确定：

在原国家标准《铁路工程结构可靠度设计统一标准》GB 50216-94中，还涉及可靠度调整系数，原理是若同一种材料性能采用相同的设计分项系数时，可能导致某些结构极限状态设计式中隐含的可靠指标与目标可靠指标有较大偏差，这时在结构极限状态设计式中增加可靠度调整系数。
考虑分项系数计算的协调和设计参数的简化，本次修订将可靠度调整系数统一到计算模型不定性系数中，不再单独罗列可靠度调整系数，但第三层次规范可以此为基础，制定符合各自需求的参数。

A.4.1  确定的组合值系数应使按分项系数表达式设计的结构或构件的可靠指标β与目标可靠指标βnom具有最佳的一致性。

▼ 展开条文说明
A.4.1  本条规定了结构或构件设计表达式中组合值系数的确定原则。
分项系数是根据目标可靠指标按照永久作用效应与主导可变作用效应的简单组合情况优选确定的。当参与组合的作用增多时，综合作用效应的概率分布将发生变化，而各个参与组合的作用效应均以其标准值相遇的概率是极小的，为使在总作用效应取值上反映这一实际情况，保持结构的可靠性水平，需根据这一概率的大小，对各参与组合的作用效应的标准值进行必要折减，这种折减系数，就是作用效应的组合值系数。
组合值系数根据作用在组合后产生的总作用效应值在设计基准期内的超越概率与考虑单一作用时相应概率趋于一致的原则确定。在作用分项系数γ_G、γ_Q和抗力分项系数γR已给定的前提下，对两种或两种以上可变作用参与组合的情况，确定的组合值系数应使按分项系数表达式设计的结构或构件的可靠指标β与目标可靠指标β_nom具有最佳的一致性。
当结构上作用两个及两个以上可变作用(荷载)时，需采用特克斯特拉(Turkstra)组合规则进行作用(荷载)效应组合，得到最不利效应组合进行结构可靠度校准。方法如下：
若某一种可变作用(荷载)取设计基准期内最大值分布时，其余n—1种作用(荷载)取相应任意时点分布：

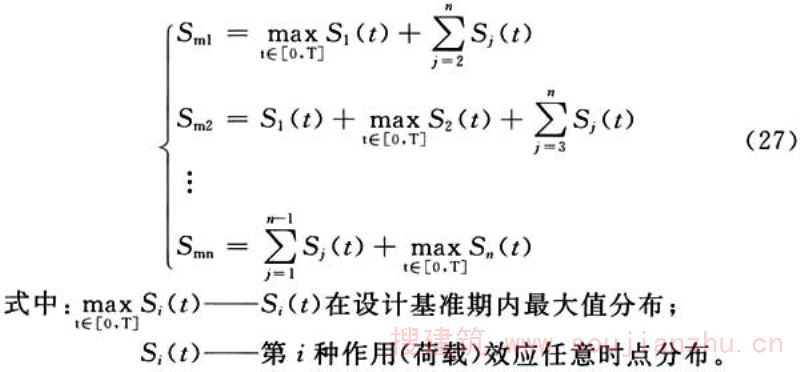
A.4.2  可变作用的组合值系数ψc可按下列步骤进行选定：

   1  选择安全等级为二级的具有代表性的若干种设计计算工况，按其对应结构的工程造价和重要性确定其权系数。

   2  按特克斯特拉(Turkstra)组合方法，求得各种设计计算工况下各个可变作用组合成的组合可变作用效应SM,J在设计基准期内最大值SMT,J的概率分布函数。

   3  将组合可变作用效应SMT,J作为一个单一的可变作用效应，根据既定的目标可靠指标按本标准附录A.3.2提供的方法或其他适当的方法，求得各种设计计算工况下结构承载能力极限状态设计式中各个永久作用效应的理论设计值SGid,J和组合可变作用效应的理论设计值SMTd,J。

   4  根据采用组合可变作用效应理论设计值SMTd,J的作用效应理论设计值与采用组合值系数的作用效应理论设计值相等的原则，确定各种设计计算状况下的理论组合值系数ψc,J，相应的组合值系数ψc,J可按下式求得：

   式中：γGi、γQ1——永久作用Gi和主导可变作用Q1的设计分项系数；

         γQj——可变作用Qj(j＝2，3，…，n)的设计分项系数。

   5  根据各种设计计算工况求得的理论组合值系数ψc,J，采用加权平均的方法确定可变作用组合值系数ψc。

▼ 展开条文说明
A.4.2  本条阐述了确定结构或构件设计表达式中组合值系数的步骤，对于不同的结构或构件，可能有所差别，可以根据具体情况适当调整。

B.1.1  永久作用标准值可按下列原则确定：

   1  结构自重标准值可按结构的设计尺寸和材料平均单位重量计算；变异性较大的结构自重可视其对结构产生的不利状态，取其概率分布为5％的低分位值或概率分布为95％的高分位值作为标准值；

   2  非承载结构部件重量标准值可按结构自重同一原则制定。当取消非承载结构部件的重量使所属结构处于不利状态时，该值可取为零；

   3  土压力标准值应根据土的平衡状态和(或)工程经验，按最不利的原则确定。当土可迁移时，土压力的消失应作为一种特殊的设计工况进行验算；

   4  预加应力标准值应考虑时间效应影响，采用永存预应力；

   5  结构施工或材料收缩、焊接等所引起的强制变形，其标准值可规定为单一值。当取消该值为不利时，该值可取为零；

   6  由不均匀沉降引起的作用标准值应按最不利组合工况确定。

▼ 展开条文说明
B.1.1  本条规定永久作用标准值的确定原则。对变异性较大的结构自重视其对结构产生的不利状态，取其概率分布为5％的低分位值或概率分布为95％的高分位值作为标准值。其他永久作用存在多样性和复杂性，需结合具体情况制定相应标准值的取值原则。
土压力标准值应按照最不利的原则确定：主动土压力可取最大值，静止土压力及被动土压力应结合工程经验确定。

B.1.2  永久作用G的概率分布类型可假设符合正态分布，其平均值G和变异系数δG可根据观测资料采用统计推断的方法确定。

▼ 展开条文说明
B.1.2  永久作用概率分布类型一般可假定服从正态分布。

B.2.1  可变作用在设计基准期内极大值(或极小值)的概率分布类型和分布参数，可根据观测资料通过统计推断的方法确定，宜按下列步骤进行：

   1  选择一个适当的单位观测期t0；

   2  记录每一个单位观测期可变作用的极大值(或极小值)Qi；

   3  以所有记录的可变作用极大值(或极小值)为基础，用概率论和数理统计学的方法，判定其概率分布类型并估计其分布参数；

   4  将判定的概率分布作为初始分布，用极值统计方法估算可变作用在设计基准期内极大值(或极小值)的概率分布类型和分布参数。

▼ 展开条文说明
B.2.1  可变作用的概率模型，为便于分析，经常被简化为平稳二项随机过程的模型，它在设计基准期内的最大值可采用经过简化后的随机变量来描述。
可变作用的标准值通常可根据它在设计基准期内最大值的统计特征值来确定，常用的特征值有平均值、标准差和变异系数。对于大多数可变作用在设计基准期内最大值的统计分布，一般假定服从极值Ⅰ型分布。当作用为风、雪等自然作用时，其标准值是在设计基准期内概率密度的最大值。对其他可变作用，一般是根据传统的取值原则，必要时也可以取较高的分位值，如对于设计地震作用，其值是相当于设计基准期为50年最大烈度分布的90％的分位值。
铁路工程结构中某些可变作用，在设计基准期内可能有一定发展，要对可能出现的较大荷载进行预测。可以根据观测的荷载乘以发展系数的方法进行预估，也可以根据国家技术发展政策以可能出现的较大技术装备引起的荷载进行预估。

B.2.2  可变作用的准永久值ψqQk按下列方法确定：

   1  记录在选定设计基准期T内可变作用值超过ψqQk的总持续时间∑ti；

   2  若∑ti与T之比η符合规定值，则ψqQk即可作为准永久值。η可根据不同性质的作用和不同的设计状况取值，并不应大于0.5。

B.2.3  可变作用的频遇值ψfQk可按下列方法之一确定：

   1  按准永久值的取值方法确定频遇值，但η应取相当小的值；

   2  按平均跨阈率(单位时间平均超越次数)确定频遇值。对铁路桥梁，可将平均跨阈率规定为每若干次列车中平均超越1次计算。

▼ 展开条文说明
B.2.2、B.2.3  可变作用的准永久值是表征其经常在结构上存在的持久部分，它是在结构长期作用效应过程中所考虑的作用代表值，即作用值被超越的总持续时间与设计基准期相比不可忽视时。
某可变作用设计基准期为t_r，当认为是各态历经的随机过程时，见图3，其超越慨率为：

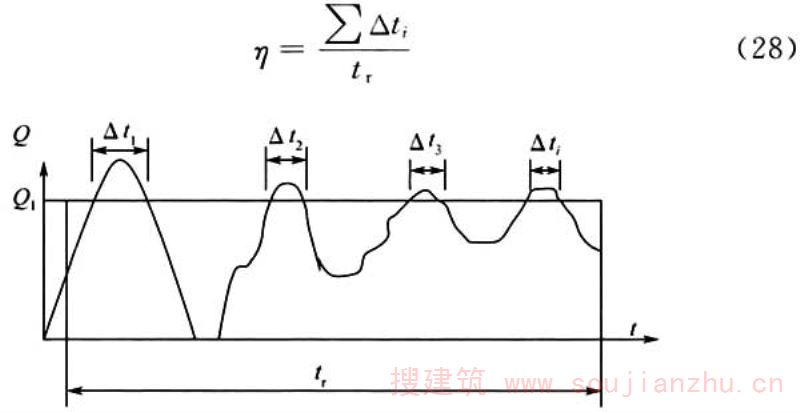
设可变荷载Q出现的非零概率为q，其任意时点分布函数为FQ(x)，x＝Q1的超越概率为：

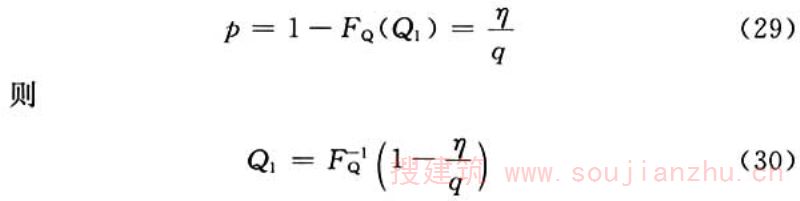
当q确定，且取η＝0.5时，ISO 2394中建议，准永久值根据在设计基准期内荷载达到和超过该值的总持续时间与设计基准期的比值为0.5确定。则Q1称为荷载的准永久值，并表示为：

式中：ψ1为准永久值系数；Qk为荷载标准值。
当q确定，且取η＝0.1时，Q1称为荷载的频遇值，相应的ψ1为频遇值系数。
对铁路列车荷载等可变作用而言，其频遇值的确定可采用第二种方法，即按平均跨阈率来确定频遇值，关于平均跨阈率的选定往往根据技术性和经济性综合考虑。
当不能确定可变作用的随机过程模型或时点分布及统计特征时，准永久值系数和频遇值系数可根据工程经验确定。

B.2.4  可变作用的组合值ψcQk可按下列方法之一确定：

   1  根据本标准A.4确定的组合值系数直接计算；

   2  可变作用的组合值ψcQk可按下式确定：

   式中：F-1Qmax(.)——可变作用设计基准期内最大值概率分布函数的反函数；

         r——设计基准期内可变作用的等时段数。

   3  当不能给出可变作用的随机过程概率模型或任意时点(或时段)概率分布时，组合值可根据工程经验或有关标准综合分析确定。

▼ 展开条文说明
B.2.4  按照Turkstra荷载组合规则，进行荷载组合时，可变荷载中的一个取设计基准期的最大值，而其他可变荷载取时点(或时段)值。荷载组合系数就是将对应于设计基准期的荷载设计值转化为对应于时点(或时段)的设计值。
对于荷载Q，荷载的设计值取为设计点(验算点处)的值。根据可靠度理论中非正态随机变量的当量正态化原则，在设计点处非正态随机变量的概率值与正态随机变量的概率值相等。
当Q为主导荷载时：

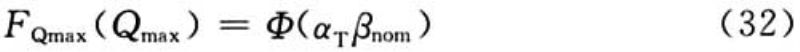
其中，F_Qmax(·)为荷载Q设计基准期T内最大值概率分布；国际标准和欧洲规范均建议α_T取0.7。
当Q为非主导荷载时：

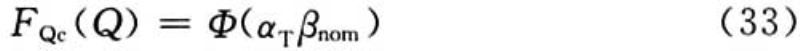
其中，F_Qc(·)为荷载Q任意时点(或时段)的概率分布；国际标准和欧洲规范均建议α_T取0.4×0.7＝0.28。

设计基准期内最大值的概率分布函数与时点(或时段)值的概率分布函数存在如下关系：

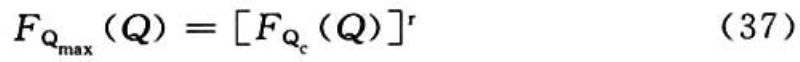
其中，r为设计基准期与时段长度的比值。分析中常采用Q_max的概率分布而不直接采用Q_c的概率分布。则荷载组合值表示为

B.3.1  以当前行车条件为基础，结构验算部位列车作用效应的概率分布函数的估算应按下列步骤进行：

   1  选择代表性的铁路区段进行调查，统计分析每趟列车通过时结构验算部位的最大作用效应Sdyn,1的概率分布函数Fsdyn,1(x)；分析应考虑机车车辆类型及其组合，机车车辆的自重、装载量及其组合，动力系数和计算模型不定性等因素；

   2  将结构验算部位产生的最大作用效应Sdyn,1的概率分布函数Fsdyn,1(x)作为初始分布，可计算铁路列车在当前行车条件下设计基准期内最大作用效应S′dyn,T的概率分布函数F′sdyn,T(y)；

   3  考虑设计基准期内机车车辆的可能发展，可按当前行车条件下求得的设计基准期内最大作用效应S′dyn,T乘以发展系数，以确定设计基准期内最大作用效应Sdyn,T的概率分布函数Fsdyn,T(y)，不同结构物可采用不同的发展系数。

B.3.2  根据预估行车条件，结构验算部位作用效应概率分布函数的估算步骤应符合下列规定：

   1  根据我国铁路技术发展政策或其他有效的预估方法，对设计基准期内的行车条件进行预估，并估算在预估行车条件下，每趟列车通过时验算部位产生的最大作用效应Sdyn,1的概率分布函数Fsdyn,1(x)；估算中应考虑机车车辆的自重、装载量及其组合的变异性，动力系数(包括其变异性)和计算模型不定性等因素，其中机车车辆的静活载效应是有上界和下界的；

   2  将结构验算部位产生的最大作用效应Sdyn,1的概率分布函数Fsdyn,1(x)作为初始分布，通过极值统计方法求得列车最大作用效应Sdyn,T的概率分布函数Fsdyn,T(y)；必要时在Sdyn,T的概率分布函数的估算中，可引入适当的计算模型不定性变量。

▼ 展开条文说明
B.3.1、B.3.2  为了统计一定条件下运营列车作用效应情况，就要对车辆荷载进行分析，确定列车作用效应分布的方法有两个，一是通过现场测试，二是理论计算。前者是对典型的铁路区段，确定每趟列车通过验算部位的最大动活载效应，将最大动活载概率分布函数作为初始分布，考虑机车车辆发展系数，通过极值统计方法得到铁路列车在设计基准期内的最大作用效应分布。后者是通过预估行车条件作为基础，再按照上述步骤得到设计基准期内的列车荷载效应概率分布，由于预估行车条件已考虑了铁路机车车辆轴重和构造、行车速度和行车密度的发展，故可不再考虑发展系数。前者缺点是缺少样本量，后者局限在于如何确保预估行车条件的准确性。

B.4.1  铁路列车疲劳荷载谱和标准荷载效应比频谱可通过疲劳列车法，按下列步骤确定：

   1  选择具有代表性的铁路线路进行运营列车的调查，将各种类型的列车归纳成几种典型的疲劳列车(如煤车、油罐车、普通货车和客车等)，并根据需要分别规定各种疲劳列车的车辆数、轴重、轴距和行车速度。对不同特征的线路，应根据其荷载特征和设计基准期内的年运量以及通过的车种(考虑发展)定出疲劳列车的组成和通过次数，形成铁路列车疲劳荷载谱。

   2  选择具有代表性的铁路结构物，计算出在设计基准期内各种疲劳列车通过时，结构或构件的荷载效应和相应的重复次数。采用雨流法等进行数据处理，编制成疲劳荷载效应谱表，以反映不同量级的荷载效应与重复次数的关系。

   3  在实际设计使用中，可将疲劳荷载效应谱中各级重复荷载效应除以结构承载能力极限状态设计中采用的铁路列车作用效应标准值，得到按疲劳列车求得的各级重复荷载效应与列车标准作用效应的比值，称为荷载效应比，并将荷载效应比与重复次数的关系编制成标准荷载效应比频谱。

B.4.2  有条件时，铁路列车疲劳荷载谱或标准荷载效应比频谱可通过实测法确定，实测法应包括下列内容：

   1  选择具有代表性的结构物，进行铁路列车作用或作用效应的测定；

   2  通过统计分析，得出结构或构件在设计基准期内各级荷载或荷载效应循环次数，并在考虑发展系数的基础上，编制相应的疲劳荷载谱或标准荷载效应比频谱。

▼ 展开条文说明
B.4.1、B.4.2  许多承受重复荷载的构件，其荷载是一种变幅重复荷载，由此而产生的荷载效应如应力、应变等也是变幅的。这一变幅荷载(或荷载效应)不能用一个单一的荷载值(或荷载效应值)表达，而需要用一个荷载谱(或荷载效应谱)予以表达。荷载谱(或荷载效应谱)的表达方式有荷载(或荷载效应)的循环次数表、循环次数直方图和循环次数曲线等。
疲劳列车模式和各类疲劳列车的运营频率是计算疲劳效应的基础。根据对不同运量等级线路的调查统计，分析制定出典型疲劳列车，将各种疲劳列车模拟通过结构物，可得疲劳荷载效应谱。标准荷载效应比频谱，是荷载谱中的疲劳荷载效应与列车竖向作用效应标准值的比值与发生次数的关系表。

C.0.1  铁路工程结构勘察设计、施工、使用和维护以及所涉及的材料和构件，应实行有效的质量管理和控制，并避免人为差错和其他不测事件。质量控制的内容、步骤和方法应在有关生产、施工和验收等规范中明确规定。

▼ 展开条文说明
C.0.1  本标准把结构可靠度(目标可靠指标)作为设计的依据，建立以概率理论为基础的极限状态方程，谋求在可持续发展前提下使结构达到预期功能的要求。结构可靠度是结构可靠性的一个定量描述，是建立在大量客观的试验和观测数据，并对结构功能函数进行不定性分析的基础上，只有结构获得质量保证，才能使结构的安全性、适用性和耐久性在设计基准期内达到设计预定的要求。为保证结构质量，则要对勘察设计、施工、使用和维护以及所涉及的材料和构件，实行有效的质量管理和控制。

C.0.2  铁路工程结构质量管理周期，应为从勘察设计、工程实施、竣工验收、使用、维护和修复直至失效的全寿命周期过程。

▼ 展开条文说明
C.0.2  铁路工程结构质量管理周期体现了全寿命(又称全生命)过程可靠性的理念。

C.0.3  铁路工程结构应按表C.0.3进行质量管理。

表C.0.3  铁路工程结构质量管理主要内容

▼ 展开条文说明
C.0.3  铁路工程结构可靠性管理阶段包括勘察设计、工程实施、竣工验收、使用、维护和修复。每个阶段都关系到铁路工程结构的全寿命可靠性，因此对每个阶段都要进行相应的质量管理。

C.0.4  铁路工程结构的质量控制应包括下列内容：

   1  勘察与设计的质量控制；

   2  材料和构件的质量控制；

   3  工程施工的质量控制；

   4  使用和维护的质量控制。

▼ 展开条文说明
C.0.4  结构可靠度的保证是有“规定条件”的，这个“规定条件”就是指正常设计、正常施工和正常使用。工程结构的勘察、设计、施工、使用和维护以及所涉及的材料和构件，是整个工程重要的实施环节，共同确保了全寿命周期的可靠性。因此，需要对上述各环节进行质量管理和控制。有关部门要把对各环节的质量要求以及质量保证中必不可少的活动或措施补充到相关的标准、规范中，对工程实行全面的质量控制。

C.0.5  铁路工程结构勘察与设计的质量控制应符合下列规定：

   1  资料齐全，数据准确，满足工程要求；

   2  设计计算假定符合规定的要求和条件；

   3  计算模型合理和数值计算正确；

   4  设计合理，结构可靠；

   5  勘察设计图纸和其他文件符合有关规定。

▼ 展开条文说明
C.0.5  铁路工程结构的勘察设计质量对结构可靠性有着首要的、直接的影响，要严格管理和控制。建立明确的责任制和严格的检查校核制度，对防止发生设计事故具有极其重要的作用。本条强调了对勘察与设计的质量控制要求。

C.0.6  铁路工程结构的材料、构件和工程施工的质量控制应包括下列内容：

   1  初步控制：通过试生产确定合理的原材料组成和工艺参数，为生产控制提出材料和构件性能的统计参数；

   2  过程控制：将生产过程或施工过程划分为若干工序，在各个工序内及若干中间生产环节进行质量检查，对工序操作和中间产品的质量，应采用统计方法进行抽查；在结构的关键部位应进行系统检查，以保证生产成品和工程结构符合设计质量要求；

   3  合格控制：按规定的质量验收标准，对材料、构件和工程进行合格检验。当材料、构件和工程按合格和不合格分类时，宜采用计数控制；材料、构件和工程施工的质量可按某些质量特征指标检定时，宜采用计量控制。

▼ 展开条文说明
C.0.6  本条给出了铁路工程结构的材料、构件和工程施工质量控制的基本内容。

C.0.7  材料宜根据统计资料，按不同质量水平划分等级。在结构设计规范与施工规范中，应对材料和构件的力学性能、几何参数等质量特征提出明确要求。材料和构件的合格质量水平，应根据规范规定的可靠性水平确定。

▼ 展开条文说明
C.0.7  材料等级一般以材料强度标准值划分。同一等级的材料采用同一标准值。无论天然材料还是人工材料，属于同一等级的不同产地和不同厂家的材料，其性能水平一般不低于规范规定的可靠指标β的要求。考虑实际应用情况，允许各有关规范根据材料和构件的特点对此指标稍做增减。

C.0.8  对生产连续性较差或各批间质量特征的统计参数差异较大的材料和构件，应针对风险制定专门的质量验收标准。

▼ 展开条文说明
C.0.8  对于生产连续性较差或各批次间质量特征的统计参数差异较大的材料和构件，很难使产品批的质量维持在合格质量水平之上，因此要按控制用户方风险率制定验收标准。计算用户方风险率时所采用的极限质量水平，可以按各类材料结构设计规范的有关要求和工程经验确定，与极限质量水平相应的用户风险率，可以根据有关标准的规定确定。

C.0.9  一批材料或构件经抽样检验判为不合格时，应根据有关质量验收标准对该批产品进行复查或重新确定其质量等级，或采取其他措施处理。

▼ 展开条文说明
C.0.9  当交验的材料或构件按质量验收标准检验判为不合格时，并不意味着这批产品一定不能使用，因为实际上存在着抽样检验结构的偶然性和试件的代表性等问题。为此，要根据有关的质量验收标准采取各种措施对产品做进一步检验和判定。例如，可以重新抽取较多的试样进行复查；当材料或构件已进入结构物时，可以直接从结构中截取试件进行复查，或直接在结构物上进行荷载试验；也允许采用可靠的非破损检验方法并经综合分析后对结构做出质量评估。对于不合格的产品允许降级使用，直至报废。

C.0.10  铁路工程施工质量应达到设计要求的结构安全和使用功能，施工单位作为工程施工质量的控制主体，应建立健全质量保证体系，对工程施工质量进行全过程控制，建设单位、监理单位和勘察设计单位、咨询单位等各方应按有关规定分工负责。

C.0.11  铁路工程结构应在设计预定的条件下使用。实际使用条件与设计预定的使用条件不同时，应进行专门的可靠性评定，必要时应采取适当的保证措施。

C.0.12  铁路工程结构使用中应规定适当的检查和维修制度，以保证结构在设计使用年限内具有要求的可靠性水平。检查形式可包括经常检查、定期检查、临时检查、专项检查、检定试验等。结构应在维修周期期间不发生显著的退化，结构设计应设置适用于结构检查和维修的设施。

▼ 展开条文说明
C.0.10～C.0.12  结构全寿命周期可靠性水平的实现是以正常设计、正常施工和正常使用为前提的，包括正常的维修和养护，即其可靠性水平与建设方、勘察设计方、施工方、监理方及运维方等密切相关，因此要对设计、施工、使用、维修和养护等进行必要的审查、检查和监督，我国有关部门和规范对此有明确规定，各方要予以遵守，按照规定分工承担各自的权责。
当铁路工程结构实际使用条件与设计预定正常使用条件不同时，要进行专门的评定。只有符合可靠性要求时才能使用，必要时要采取适当的保证措施。
维修养护制度是保证结构全寿命过程可靠性的重要环节，需重视并加以完善。维修周期要保证结构性能不发生显著退化。

C.0.13  铁路工程结构宜逐步建立工程数据统计和处理分析平台，有条件时可基于BIM技术进行关联和共享，收集与可靠性密切相关的数据信息，并及时评估分析，修正相关设计参数和结构可靠性水平。

▼ 展开条文说明
C.0.13  极限状态设计法是以大量的统计数据为基础，为便于各专业进行有效的参数统计，科研项目“铁路工程结构极限状态设计标准转轨关键技术研究”(2012G014-A)对工程数据敏感性进行研究，研究建议工程结构数据的筛选可采用经验判断和敏感性分析相结合的方法，并对桥梁、隧道、路基、轨道四个专业的数据进行筛选，形成了铁路工程结构数据的初步统计方案。科研项目“铁路工程数据统计和处理分析平台基础研究”(Z2012-065)探索了铁路工程数据采集范围、采集渠道，搭建了工程数据采集、统计和评估分析的模拟平台，提出了铁路工程数据分析平台的总体技术框架和建设实施方案。
为实现可靠性设计规范的可持续发展，宜建立工程结构数据统计和处理分析平台，对设计阶段、建造过程和运维期间关键参数进行采集、传输、存储和评估分析，有条件时可基于BIM(Building information modelling)技术进行数据的关联和共享，将专业需求与云计算、物联网、大数据等信息技术充分融合，逐步实现从数据到信息、知识直至智慧的进阶，从而达到修正目标可靠指标及相关参数指标的目的，指导规范的修订，这也符合结构可靠性理论的基本要求。只有全面掌握关键数据，才能实行精细化的质量管理和控制，促进质量管理的有机循环。

D.1.1  既有铁路工程结构的可靠性评定应在保证结构性能的前提下，尽量减少对既有结构的处置工作量。

▼ 展开条文说明
D.1.1  既有结构可靠性评定的基本原则是确保结构现役性能不发生进一步恶化，在此前提下开展相应的评定工作，同时应尽量考虑后续评定工程量。

D.1.2  既有铁路工程结构的可靠性评定可分为安全性评定、适用性评定和耐久性评定，必要时尚应进行抗灾害能力评定。

D.1.3  既有铁路工程结构的可靠性评定，可按照本标准给出的概率极限状态设计方法进行。没有按极限状态法设计的结构可直接通过可靠指标进行评定。既有结构设计时采用的其他原则，宜作为指导性的参考资料。

D.1.4  既有铁路工程结构可靠性评定采用的基本变量应按下列要求取值：

   1  结构几何尺寸：若原设计文件有效，且未发生尺寸改变或出现尺寸偏差的迹象，则分析时应采用原设计确定的名义尺寸；但这些尺寸须经足够范围的检测加以验证；

   2  荷载作用：应引入与实际情况相应的荷载作用；

   3  材料性能：应按结构实际情况考虑。若原设计文件有效，且不怀疑材料有严重退化或原设计、施工有偏差，则取用原设计的特征值。必要时应进行破损或非破损检测，并采用统计方法确定：

   4  计算模型：除非对结构性能另有说明，模型不定性应按原设计考虑。在某些情况下，模型参数、系数和设计假定可根据对既有结构的实测结果来建立。

▼ 展开条文说明
D.1.4  既有结构显著特点是作用已明确，进行可靠性评定时，需引入与实际情况相应的荷载作用；同时由于服役期间外界条件的影响，还要对结构的几何尺寸、材料性能进行验证统计；除非对结构性能另有说明(如损坏)，模型不定性仍按原设计考虑；既有结构的计算参数如风压系数、有效宽度等可根据对既有结构的实测结果来确定。

D.1.5  既有铁路工程结构的可靠性评定应按下列步骤进行：

   1  明确评定的对象、内容和目的；

   2  通过调查、检测获得与结构上的作用或作用效应及结构实际性能或状况的相关信息，并作出以下方面的结论或推论：

       1)试验荷载下被试构件的承载力；

       2)其他同类构件的承载力；

       3)其他荷载条件下的承载力；

       4)结构体系的性能。

   3  实际结构的可靠性应按下列方法进行估计：

       1)修正各变量的概率分布和设计参数，直接比较作用效应与限值(如裂缝宽度、位移)；

       2)估算可靠指标或失效概率，与预期值比较。

   4  提出评定报告。

▼ 展开条文说明
D.1.5  既有结构的可靠性评定时，要尽量获得结构性能的信息，以便于对结构性能的实际状况进行评定。

D.2.1  既有铁路工程结构的安全性评定，应包括结构体系和构件布置、连接和构造、承载力三个评定项目。

▼ 展开条文说明
D.2.1  既有铁路工程结构的安全性是指直接影响人员或财产安全的评定内容。为了便于评定工作的实施，本条把结构安全性的评定分成结构体系和构件布置连接和构造、承载力三个评定项目。

D.2.2  既有铁路工程结构的结构体系和构件布置应以现行结构设计标准的要求为依据进行评定。

▼ 展开条文说明
D.2.2  铁路工程结构体系和构件布置若存在问题，相应安全事故出现的概率就非常大。现行结构设计规范对结构体系和构件布置的要求是当前工程界普遍认同的下限要求，既有结构的结构体系在满足相应要求的情况下可以评为符合要求。结构安全性评定中的结构体系和构件布置要求，不包括结构抗灾害的特殊要求。

D.2.3  既有铁路工程结构的连接和与安全性相关的构造应以现行结构设计标准的要求为依据进行评定。

▼ 展开条文说明
D.2.3  连接和构造存在问题是结构失效的重要原因，这包括强度破坏、疲劳破坏、耐久性降低等。现行结构设计规范对连接和构造的要求是当前工程界普遍认同的下限要求，既有结构的连接和构造在满足相应要求的情况下可以评为符合要求。本条所提到的构造仅涉及与构件承载力相关的构造。

D.2.4  结构体系和构件布置、连接和构造的评定结果满足本标准D.2.2和D.2.3条要求时，其承载力可根据结构的不同情况采取下列方法进行评定：

   1  基于结构良好状态的评定方法；

   2  基于分项系数或安全系数的评定方法；

   3  基于可靠指标调整抗力分项系数的评定方法；

   4  基于荷载检验的评定方法；

   5  其他适用的评定方法。

▼ 展开条文说明
D.2.4  本条提出的承载力评定方法，前提是要求既有铁路工程结构的结构体系和构件布置、连接和构造要符合现行结构设计规范的要求。

D.2.5  结构处于良好使用状态时，宜采用基于结构良好状态的评定方法，此时对同时满足下列要求的结构，可评定其承载力符合规定。

   1  结构未出现明显影响结构正常使用的变形、沉降、裂缝、位移、振动等适用性问题；

   2  在评估使用年限内，结构上的作用和环境不会发生显著的变化。

▼ 展开条文说明
D.2.5  本条提出基于结构良好状态的评定原则，结构未达到正常使用极限状态的限值且结构上的作用不会出现明显的变化，结构的安全性可以得到保证，当既有结构经历了相应的灾害而未出现达到正常使用极限状态限值的现象，也可以认定该结构可以抵抗这种灾害的作用。

D.2.6  采用基于分项系数或安全系数的方法评定时，对同时满足下列要求的结构，可评定其承载力符合规定。

   1  构件的承载力应按现行结构设计标准提供的结构计算模型确定。评定时模型采用的指标或参数可按下列实际情况进行调整：

       1)构件材料强度的取值，宜以实测数据为依据，按现行结构检测标准规定的方法确定；

       2)计算模型的几何参数，可按构件的实际尺寸确定；

       3)在计算分析构件承载力时，应考虑不可恢复性损伤的不利影响；

       4)经过验证后，在计算模型中可增补对构件承载力有利因素的实际作用。

   2  作用和作用效应按国家现行标准或铁路现行标准的相关规定确定。评定时可进行下列参数或分析方法的调整：

       1)永久作用应以现场实测数据为依据，按现行铁路工程结构相关规定的方法确定；

       2)部分可变作用可根据评估使用年限情况采用荷载调整系数；

       3)在计算作用效应时，应考虑尺寸偏差和安装偏差等的不利影响；

       4)应按可能出现的最不利作用组合确定作用效应。

   3  按上述方法计算得到的构件承载力不小于作用效应或安全系数不小于有关结构设计标准的要求。

▼ 展开条文说明
D.2.6  本条提出基于结构分项系数或安全系数的评定原则。
结构的设计阶段有三类问题需要结构设计规范确定，其一为规律性问题，结构设计规范用计算模型反映规律问题；其二为离散性问题，结构设计规范用分项系数或安全系数解决这个问题；其三为不确定性问题，结构设计规范用额外的安全储备解决设计阶段的不确定性问题，这类储备一般不计入规范规定的安全系数或分项系数。对于既有结构来说，设计阶段各种因素的不确定性降低，有些可以通过检验与测试定量确定。当这些因素明确后，在既有结构承载力评定中可以适度利用这些储备，在保证分项系数或安全系数满足现行规范要求的前提下，尽量减少结构的加固工程量。
例如，关于构件材料强度的取值，可以利用混凝土的后期强度和钢材实际屈服点应力高于结构规范提供的强度标准值的部分；现行结构设计规范计算公式中未考虑对构件承载力有利因素，如纵向钢筋对构件受剪承载力的有利影响等。
既有结构还有一些已经确定的因素是对构件承载力不利的，如轴线偏差、尺寸偏差以及不可恢复性损伤(钢筋锈蚀)，这些因素也要在承载力评定时考虑。

D.2.7  构件的实际承载力及其变异系数确定时，可采用基于可靠指标调整抗力分项系数的评定方法，此时对同时满足下列要求的一批构件，可评定其承载力符合要求。

   1  作用效应的计算，符合本标准D.2.6的规定；

   2  根据结构构件承载力的实际变异情况调整抗力分项系数；

   3  按上述原则计算得到的承载力不小于作用效应。

▼ 展开条文说明
D.2.7  当构件的承载能力及变异系数为已知时，计算模型中承载力的某些不确定储备可以利用，具体的方法是在保证可靠指标满足要求的前提下适度调整分项系数。

D.2.8  具备相应条件的结构或构件，可采用基于荷载检验的评定方法，此时对同时满足下列要求的结构或构件，可评定其承载力符合规定。

   1  检验荷载的形式应与结构承受主要作用的情况基本一致，检验荷载不应使结构或构件出现不可逆的变形或损伤；

   2  荷载检验及相应的计算分析结果符合有关标准的规定。

▼ 展开条文说明
D.2.8  荷载检验是确定构件承载力的方法之一，本条提出荷载试验确定承载力的原则。检验荷载值要通过预先的计算估计，并在检验时逐级进行控制，避免产生结构或构件的过大变形或损伤。
对于检验荷载未达到设计荷载的情况，可以采取辅助计算分析的方法实现。

D.2.9  结构或构件的承载力评定不符合要求时，应提出采取加固措施的建议，必要时，也可提出对其限制使用的要求。

▼ 展开条文说明
D.2.9  对承载力评定为不符合要求的结构或构件，需采取相应的加固措施，当加固措施未发挥效用之前，可以对其使用条件进行限制(如限速)或实施临时加固措施。

D.2.10  铁路桥涵的安全性评定可包括桥梁荷载评定，下部结构、上部结构各构件之间连接和结构构造的承载力评定等。

D.2.11  铁路隧道的安全性评定可包括衬砌、洞门、隧道支挡结构荷载评定，隧道围岩及衬砌结构、隧底处理和加固防护措施，衬砌、洞门、隧道支挡结构及各构件之间连接和结构构造的承载力评定等。

D.2.12  铁路路基的安全性评定可包括路基结构上的荷载评定，路基及支挡结构、地基处理和加固防护措施的承载力评定等。

D.2.13  铁路轨道的安全性评定可包括钢轨、轨枕和道床上的荷载评定，轨道主体结构(轨枕、道床、底座板、轨道板等)承载力评定，脱轨系数和轮重减载率评定，轨道主体结构各构件之间的连接和结构构造的承载力评定等。

▼ 展开条文说明
D.2.10～D.2.13  提出了既有铁路工程结构中的桥涵、隧道、路基和轨道安全性评定的具体内容和方向，方便工程师理解和操作。

D.3.1  铁路工程结构安全性得到保证的情况下，对影响结构正常使用的变形、裂缝、位移、振动等适用性问题，应以现行结构设计标准的要求为依据进行评定，但在下列情况下可根据实际情况调整或确定正常使用极限状态的限值。

   1  已出现明显的适用性问题，但结构或构件尚未达到正常使用极限状态的限值；

   2  相关标准提出的质量控制指标不能准确反映结构适用性状况。

▼ 展开条文说明
D.3.1  适用性的考虑是在安全性前提下进行的。以裂缝为例，有些裂缝出现是构件承载力不满足要求的标志，此时不能简单地看成适用性问题；只有在安全性得到保障的前提下，才能评定裂缝对结构的适用性构成影响。

D.3.2  已经存在超过正常使用极限状态限值的结构或构件，应提出处理意见并及时实施。

▼ 展开条文说明
D.3.2  本条提出存在适用性问题的结构需要处理。需要注意的是，适用性问题的处理并非一定要采取提高构件承载力的加固措施。

D.3.3  未达到正常使用极限状态限值的结构或构件，宜评估使用年限内结构的适用性，并遵守下列原则：

   1  评定时可采用现行结构设计标准提供的计算模型，模型中的指标和参数应进行符合结构实际情况的调整；

   2  在条件许可时，可采用荷载检验或现场试验的评定方法；

   3  适用性评定为不满足要求的结构或构件，应提出相应的处理措施。

▼ 展开条文说明
D.3.3  本条提出未达到正常使用极限状态限值的结构或构件的适用性评定原则。

D.3.4  铁路桥涵的适用性评定可包括桥梁刚度评定，下部结构及上部结构变形评定，裂缝开展宽度评定等。

D.3.5  铁路隧道的适用性评定可包括衬砌、洞门结构及隧道底部变形评定，裂缝开展宽度评定等。

D.3.6  铁路路基的适用性评定可包括地基变形评定，路基本体变形评定，高速铁路上支挡结构变形评定等。

D.3.7  铁路轨道的适用性评定可包括轨道结构静态和动态几何形位变形评定，无砟轨道混凝土结构裂缝开展宽度评定，列车运行时车体振动加速度评定等。

▼ 展开条文说明
D.3.4～D.3.7  规定了既有铁路工程结构中的桥涵、隧道、路基和轨道适用性评定的具体内容和方向，方便工程师理解和操作。

D.4.1  既有结构的耐久性评定应以判定结构相应耐久年限与评估使用年限之间关系为目的。

▼ 展开条文说明
D.4.1  结构的耐久年限为结构在环境作用下出现相应正常使用极限状态限值或标志的年限，判定耐久年限是否大于评估使用年限是结构耐久性评定的目的。

D.4.2  结构在环境作用下，正常使用极限状态的限值或标志应根据下列情况确定：

   1  结构或构件出现尚未明显影响承载力的表面损伤；

   2  结构或构件材料的性能劣化，使其产生脆性破坏的可能性增大。

▼ 展开条文说明
D.4.2  本条提出确定与耐久性有关的极限状态限值或标志的原则，耐久性属于正常使用极限状态的范畴。达到与耐久性有关的极限状态标志或限值表明需对结构或构件采取修复措施。

D.4.3  既有结构的耐久年限推定，应将环境作用效应和材料性能相同的结构或构件作为一个批次。结构体系中各附属结构构件要考虑与主体结构寿命周期的配套，应提出适宜的维护处理及更换建议。

▼ 展开条文说明
D.4.3  环境是造成构件材料性能劣化的外界因素，材料性能体现其抵抗环境作用的能力，将环境作用效应和材料性能相同的构件作为一个批次进行评定，有利于运营单位采取合理的修复措施。

D.4.4  评定批结构或构件的耐久年限，可根据结构已经使用的时间、材料相关性能变化的状况、环境作用情况和材料性能劣化的规律推定。

▼ 展开条文说明
D.4.4  本条提出构件耐久年限的评定方法。

D.4.5  结构耐久年限小于评估使用年限时，应提出适宜的维护处理建议。

▼ 展开条文说明
D.4.5  对于耐久年限小于评估使用年限的构件，应提出相应的维护处理建议，建议措施应实现材料劣化速率的降低，耐久使用年限的延长等。

D.4.6  铁路桥涵的耐久性评定可包括下部结构以及上部结构的完整性评定，环境作用下结构材料性能劣化程度的评定等。耐久性状况包括混凝土碳化、混凝土中氯离子含量及侵入度、混凝土中硫酸盐浓度及侵入度、钢筋锈蚀程度、预应力锚头锈蚀程度、钢构件锈蚀程度等状况。

D.4.7  铁路隧道的耐久性评定可包括衬砌、洞门、隧道支挡结构的完整性评定，环境作用下围岩变性、结构材料性能劣化程度的评定等。耐久性状况包括混凝土中氯离子含量及侵入度、混凝土中硫酸盐浓度及侵入度、钢筋锈蚀程度及围岩岩性改变等状况。

D.4.8  铁路路基的耐久性评定可包括路基、支挡结构和加固防护结构的完整性评定，基床结构和边坡等的长期稳定性评定，环境作用下结构材料性能劣化程度的评定等。耐久性状况包括混凝土中氯离子含量及侵入度、混凝土中硫酸盐浓度及侵入度、钢筋锈蚀程度、预应力锚索腐蚀等状况。

D.4.9  铁路轨道的耐久性评定可包括无砟轨道轨道板／道床板、底座板及有砟轨道混凝土轨枕、道床等结构的完整性评定，环境作用下结构材料性能劣化程度的评定，混凝土表面磨损程度评定等。耐久性状况包括混凝土碳化、混凝土中氯离子含量及侵入度、其他化学介质侵蚀、混凝土冻融破坏程度和碱-集料反应、钢筋锈蚀程度等状况。

▼ 展开条文说明
D.4.6～D.4.9  规定了既有铁路工程结构中的桥涵、隧道、路基和轨道耐久性评定的具体内容和方向，方便工程师理解和操作。

D.5.1  既有结构的抗灾害能力宜从结构体系和构件布置、具体结构在结构体系中的地位作用、连接和构造、承载力、防灾减灾和防护措施等方面进行综合评定。

▼ 展开条文说明
D.5.1  本条提出既有铁路工程结构的抗灾害能力评定的项目。

D.5.2  地震、台风、雨雪和水灾等自然灾害的作用可以确定时，宜通过结构安全性校核评定其抗灾害能力。

▼ 展开条文说明
D.5.2  若对于部分灾害如地震作用已经有了具体的规定，既有结构抗灾害的能力要按照这些规定进行评定。

D.5.3  发生在结构局部的撞击、火灾等偶然作用，宜通过评价减小其偶然作用及作用效应的措施、结构不发生与起因不相称的破坏和减小偶然作用影响范围的措施等，评定其抗灾害能力。

▼ 展开条文说明
D.5.3  对于不能准确确定作用或作用效应的灾害，需评价减小灾害作用及作用效应的措施及减少灾害影响范围和破坏范围等措施。
减小偶然作用及作用效应的措施包括防爆与泄爆措施、防撞击和抗撞击措施、控制可燃物质的措施与消防设施等。
减小偶然作用影响范围的措施包括结构变形缝设置和防止发生次生灾害的措施等。

D.5.4  铁路工程结构不可抗御的灾害，应评价其预警措施和疏散措施等。

▼ 展开条文说明
D.5.4  当山体滑坡和泥石流等灾害不能规避时，既有结构应有灾害的预警措施和人员疏散措施。

D.5.5  铁路桥涵的抗灾害能力评定可包括抗风性能评定、抗震性能评定、抗撞击能力评定、抗洪能力评定、抗泥石流能力评定、抗火灾能力评定、抗雷击能力评定、抗危岩落石能力评定等。

D.5.6  铁路隧道的抗灾害能力评定可包括衬砌、洞门、隧道支挡结构的抗震性能评定，抗火灾能力评定，洞门、隧道支挡结构抗危岩落石能力评定等。

D.5.7  铁路路基的抗灾害能力评定可包括路基及支挡结构的抗震性能评定、抗洪能力评定、抗泥石流能力评定、抗滑坡能力评定、抗雪害能力评定和抗风沙能力评定、抗危岩落石能力评定等。

D.5.8  铁路轨道的抗灾害能力评定可包括有砟轨道、无砟轨道等结构的抗撞击能力评定、抗震性能评定和抗雪害能力评定等，并应对轨道监测预警措施做出评价。

▼ 展开条文说明
D.5.5～D.5.8  规定了铁路工程结构中的桥涵、隧道、路基和轨道抗灾害能力评定具体内容和方向，方便工程师理解和操作。

本标准用词说明

1 为便于在执行本标准条文时区别对待，对要求严格程度不同的用词说明如下：

1)表示很严格，非这样做不可的：

正面词采用“必须”，反面词采用“严禁”；

2)表示严格，在正常情况下均应这样做的：

正面词采用“应”，反面词采用“不应”或“不得”；

3)表示允许稍有选择，在条件许可时首先应这样做的：

正面词采用“宜”，反面词采用“不宜”；

4)表示有选择，在一定条件下可以这样做的，采用“可”。

2 条文中指明应按其他有关标准执行的写法为：“应符合……的规定”或“应按……执行”。

引用标准名录

《铁路工程抗震设计规范》GB 50111